Prove que, quando um raio de luz incide sobre um espelho plano que gira em um ângulo em torno de um eixo perpendicular ao plano de incidência, o raio refletido gira em um ângulo igual a .
Passo 1
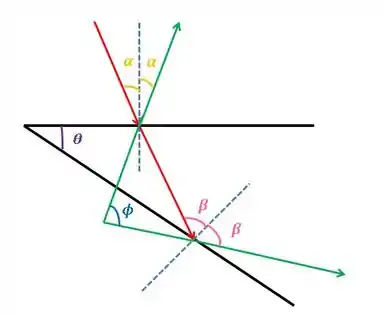
Show. Em preto está o espelho, numa posição inicial e depois girado de . Em vermelho temos os raios incidentes, e em verde os refletidos. Como queremos informação dos raios refletidos, prolongamos eles e o que queremos provar é que o . Show?
Ah! E as retas tracejadas azuis são as normais em relação a superficie do espelho.
Vamos lá então!
Passo 2
Vamos tirar algumas relações dos triângulos que aparecem.
Primeiro desse aqui:
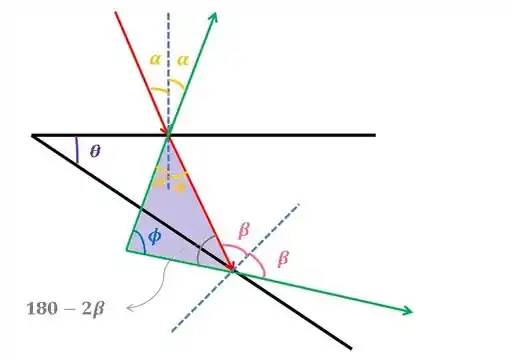
Sabemos que a soma dos ângulos internos de um triangulo é . Olhando para o triangulo destacado.
Show! Guarda essa relação.
Passo 3
Agora, vamos olhar para esse triangulo aqui:
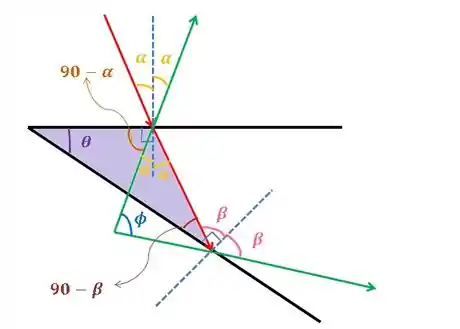
Marquei bem os ângulos retos (que vem das normais), pois usamos eles para indicar aqueles ângulos que escrevi ali na figura.
Então, ainda usando a soma dos ângulos internos de um triângulo, temos:
Daí
Vamos substituir essa relação lá na equação do passo anterior:
Então:
Uhuul!
Resposta
Ei, a resposta está no passo a passo :)