Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 5.1 - Ex. 5
Um quadro está suspenso em uma parede por dois fios ligados em seus cantos superiores. Se os dois fios fazem o mesmo ângulo com a vertical, qual deve ser o ângulo se a tensão em cada fio for igual a do peso do quadro? (Despreze o atrito entre a parede e o quadro.)
Passo 1
Fala galera! Beleza?! Bora resolver essa questão!
Nós temos um quadro suspenso em uma parede por dois fios que fazem o mesmo ângulo com a vertical e precisamos determinar o ângulo se a tensão em cada fio for igual a do peso do quadro.
Vamos construir um diagrama de corpo livre do sistema pra entender melhor:
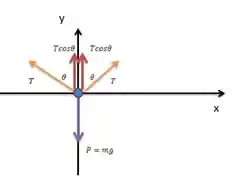
Observe que duas forças agem sobre o quadro: a força tensora (em laranja) e a força peso (em roxo). Além disso, temos que os dois fios fazem o mesmo ângulo com a vertical.
As componentes de interesse são as verticais. Temos que as componentes verticais dos dois fios (representadas em vermelho) se somam e juntas contrabalançam a força peso. Então, vamos usar a segunda lei de Newton para fazer o somatório dessas forças e igualar a zero, para que o sistema esteja equilíbrio:
Assim, vamos encontrar o valor do ângulo através das componentes da tensão .
Vamos lá!
Passo 2
O sistema todo está em equilíbrio, então a resultante das forças deve ser zero. Assim, somando as componentes verticais, temos:
Como tensão em cada fio é igual a do peso do quadro, temos: . Substituindo na equação ali em cima, ficamos com:
Isolando o cosseno do ângulo:
E calculando o arco cosseno, temos:
Assim o ângulo formado com a vertical pelos fios é .
Valeu, galera! Até a próxima! 😉