Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 5.Problemas - Ex. 61
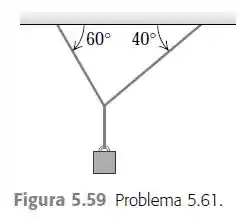
Duas cordas estão conectadas a um cabo de aço que segura um peso suspenso, como indicado
na Figura 5.59. a) Desenhe um diagrama do corpo livre mostrando as forças que atuam sobre
o nó que liga as duas cordas ao cabo de aço. Com base no diagrama de força, qual das duas cordas terá a maior tensão? b) Se a tensão máxima que cada corda pode sustentar sem se romper é de , determine o valor máximo do peso pendente que essas cordas podem suportar com segurança. Ignore o peso das cordas e do cabo de aço.
Passo 1
Eaee, belezinha?? Bom... o enunciado nos dá a seguinte figura que representa duas cordas que estão conectadas a um cabo de aço que segura um peso suspenso.
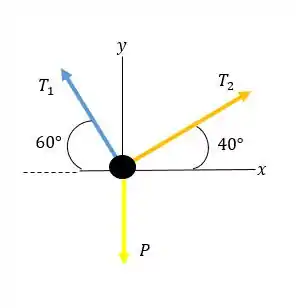
Queremos desenhar o diagrama de corpo livre, ou seja, temos que analisar todas as forças em todas as direções do corpo:
- O peso está suspenso, portanto não temos uma força normal, , agindo sobre ele.
- Em cada corda existe uma tração, que vamos denominal-as como e .
- O bloco possui uma massa, logo temos a força peso para baixo.
Em seguida o enunciado também nos pede para determinar o valor máximo do peso pendente que essas cordas podem suportar com segurança.
Para isso, a questão nos dá como dado que a tensão máxima que cada corda pode sustentar sem se romper é de .
Passo 2
- Desenhando as forças que atuam sobre o bloco temos:
- Agora vamos achar o valor máximo do peso pendente. é mais vertical, então suporta mais peso e é maior. Então, vamos aplicar a segunda lei de Newton para verificar isso:
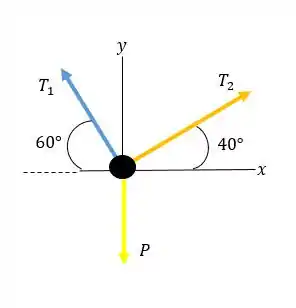
Passo 3
Onde são todas as forças em , é a massa e é a aceleração.
Lembrando que a aceleração no eixo é zero, pois o bloco não está se movimento ao longo dele. Aplicando a Lei ao nosso sistema:
Relacionando as e , ficamos com,
O problema disse que a tensão máxima suportada é de Então é maior:
Então:
