Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 6.Exercícios e Problemas - Ex. 29

Um vergalhão de aço com 1.000   k g é sustentado por duas cordas. Qual é a tensão em cada uma delas?

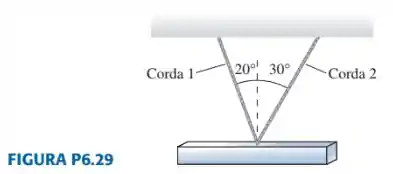
Passo 1

Vamos fazer um diagrama de corpo livre para o vergalhão de aço:

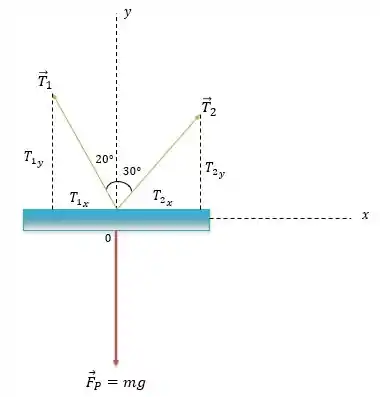
Então temos a força peso e a tensão das duas cordas,   T → 1 e T → 2 atuando no vergalhão.

Podemos decompor as tensões em componentes x e y como mostra o diagrama:

T 1 x = - T 1   s e n   20 °

T 1 y = T 1 cos ⁡ 20 °

T 2 x = T 2   s e n   30 °

T 2 y = T 2 cos ⁡ 30 °

Sempre lembrando daquele macete: COlada – COsseno, SEparada – SEno

Passo 2

O vergalhão está em equilíbrio, então o somatório das forças nas duas direções tem que ser zero:

∑ F x = 0

∑ F y = 0

Para o eixo x :

T 2 x + T 1 x = 0

T 2   s e n   30 ° - T 1   s e n   20 ° = 0

T 2   s e n   30 ° = T 1   s e n   20 °

Temos que:

s e n   30 ° = 1 2 = 0,5

s e n   20 ° = 0,34

Então:

0,5   T 2 = 0,34   T 1  

T 2 = 0,34 0,5 T 1

T 2 = 0,68   T 1

Passo 3

Agora para o eixo y :

T 1 y + T 2 y - F P = 0

T 1 cos ⁡ 20 ° + T 2 cos ⁡ 30 ° - m g = 0

T 1 cos ⁡ 20 ° + T 2 cos ⁡ 30 ° = m g

Temos que:

cos ⁡ 30 ° = 3 2 = 0,866

cos ⁡ 20 ° = 0,94  

m = 1000   K g

g = 9,8   m / s 2  

Então:

0,94   T 1 + 0,866   T 2 = 1000   x   9,8

0,94   T 1 + 0,866   T 2 = 9   800

Passo 4

Agora podemos pegar as equações que encontramos para o eixo x e para o eixo y e resolver um sistema:

T 2 = 0,68   T 1

0,94   T 1 + 0,866   T 2 = 9   800

Vamos substituir a primeira equação na segunda:

0,94   T 1 + 0,866   0,68   T 1 = 9   800

0,94   T 1 + 0,589   T 1 = 9   800

T 1 0,94 + 0,589 = 9   800

T 1 = 9   800 0,94 + 0,589  

T 1 = 6   409   N

Agora que achamos T 1 , podemos substituir esse valor na primeira equação e encontramos T 2 :

T 2 = 0,68   T 1

T 2 = 0,68   x   6   409

T 2 = 4   358   N

E prontinho =)

Resposta

T 1 = 6   409   N

T 2 = 4   358   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para o sistema das Figuras 4-41a, 4-41b e 4-41c, encontre as massas e as tensões desconhecidas.
Arcos de balão são uma decoração encontrada em feiras e comemorações. Prende-se balões cheios de hélio a uma corda fixa ao chão pelas extremidades. A ascensão dos balões levanta a estrutura em uma for
Um bloco de massa m está sendo levantado verticalmente por uma corda uniforme de massa M e comprimento L . A corda está sendo puxada para cima por uma força aplicada em sua extremidade superior, e a c
Um bloco de 10 kg está suspenso do teto de um elevador por uma corda feita para aguentar uma tensão de 150 N. Pouco depois do elevador começar a subir, a corda se rompe. Qual foi a mínima aceleração d
Um objeto de 40,0k g é suportado por uma corda vertical. A corda e o objeto são acelerados para cima, a partir do repouso, até atingir uma rapidez de 3,50m / s em 0,700s ; (a) Desenhe o diagrama de co