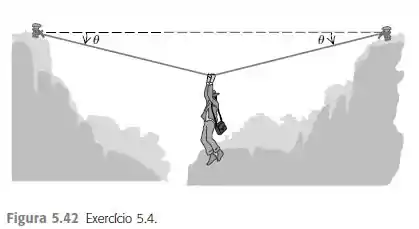
Um arqueólogo aventureiro passa de um rochedo para outro deslocando-se lentamente com as mãos por meio de uma corda esticada entre os rochedos. Ele para e fica em repouso no meio da corda (Figura ). A corda se romperá se a tensão for maior do que e se a massa do nosso herói for de .
b) Qual deve ser o menor valor de para a corda não se romper?
Passo 1
Fala galera! Beleza?! Bora resolver essa questão!
Nós temos um arqueólogo aventureiro que tá pendurado numa corda, passando de um lado para o outro. A gente sabe que ele tem massa de , que ele para e fica em equilíbrio no meio da corda e que a corda vai se romper se a tensão for maior que .
Vamos fazer um diagrama de forças para entender melhor a situação:
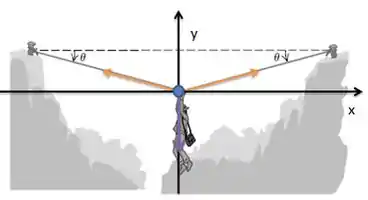
Nós queremos achar (a) a tensão na corda, quando o ângulo for e (b) o menor valor de pra essa corda não se romper. Pra isso, vamos usar segunda lei de Newton, na forma:
Assim, somaremos todas as forças presentes e encontraremos as variáveis pedidas. Vamos lá!
Passo 2
Observe que as forças tensoras da figura anterior estão representadas em laranja e formam um ângulo com o eixo . Como o arqueólogo está parado, todo o sistema está em equilíbrio. E a força peso está representada em roxo.
Na horizontal temos apenas as componentes horizontais das tensões (em cada metade da corda):
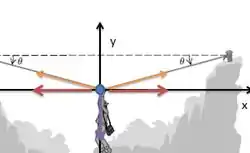
Elas estão representadas em vermelho e podemos ver que possuem módulos iguais e direção opostas, sendo assim, elas se cancelam.
E as componentes verticais? Bom, saca só elas no diagrama:
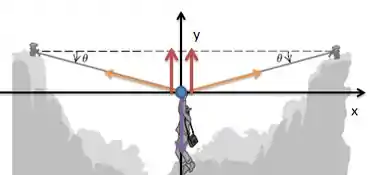
Também as representamos em vermelho. Na direção vertical elas se somam! E são contrabalançadas com a força peso do arqueólogo!
Assim, a componente vertical da tensão é , então pela segunda lei, temos:
E isolando na equação, obtemos:
O peso dele é e como podemos calcular a tensão na corda fazendo:
Passo 3
Agora o problema quer o ângulo máximo para evitar a ruptura. A tensão m��xima na corda é de . Do passo anterior temos uma relação para a tensão e o seno do ângulo que é dada por:
Nesse caso e o peso do arqueólogo segue sendo . Então, é só substituir na equação:
Isolando o seno do ângulo:
Então, calculando o arco seno que satisfaz essa equação, temos:
Valeu, galera! Até a próxima! 😉