Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 21.1 - Ex. 76

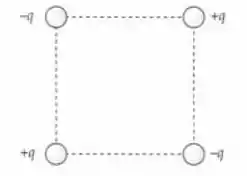
Quatro cargas puntiformes de mesma magnitude estão dispostas nos vértices de um quadrado de lado L , como mostra a Figura 21-45. (a) Determine o módulo a direção e o sentido da força exercida na carga que está no vértice inferior esquerdo pelas outras três cargas. (b) Mostre que a direção do campo elétrico no ponto médio de um dos lados do quadrado é paralela à aresta, ele aponta para a carga negativa e tem módulo E dado por E = k 8 q 2 L 2 1 - 1 5 5 .

Passo 1

  1. Veja o esquema a seguir:

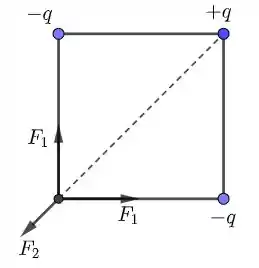
    2. Notemos que a distância entre as cargas + q é a diagonal do quadrado, que vale

    D = 2 L

    Temos que

    F 1 = k q 2 L 2

    e

    F 2 = k q 2 D 2 = k q 2 2 L 2

    A força resultante entre as forças F 1 é:

    F r 1 = F 1 2 + F 1 2 = 2 F 1 = 2 k q 2 L 2

    Note que F r 1 aponta na direção da diagonal do quadrado. Logo, a força resultante total é:

    F r = F r 1 - F 2 = 2 k q 2 L 2 - k q 2 2 L 2 = k q 2 L 2 2 - 1 2

    Sendo que a direção é apontando da carga + q inferior para a carga + q superior.

    Passo 2

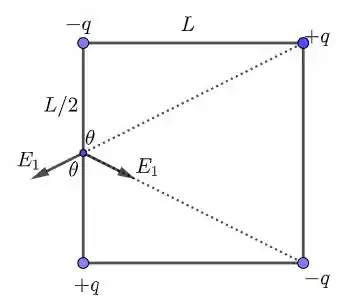
  2. Vamos calcular o campo elétrico entre + q e - q .

Notemos que o campo resultante é para baixo. A resultante é:

E r 1 = 2 E 1 cos ⁡ θ

onde

cos ⁡ θ = L / 2 L / 2 2 + L 2 = L / 2 5 L / 2 = 1 5

Assim,

E r 1 = 2 1 5 k q 2 5 L 2 / 4 = 8 5 5 k q 2 L 2

e E r 1 aponta na direção + q .

Agora, tanto + q e - q fazem um campo elétrico de módulo

E 2 = k q 2 L / 2 2 = 4 k q 2 L 2

Assim, a resultante entre esses campos elétricos é:

E r 2 = 2 E 2 = 8 k q 2 L 2

sendo que essa força aponta para - q . Segue que

E r = E r 2 - E r 1 = 8 k q 2 L 2 1 - 1 5 5

Resposta

  1. k q 2 L 2 2 - 1 2
  2. 8 k q 2 L 2 1 - 1 5 5
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um próton se desloca horizontalmente da esquerda para a direita a 4,5x10 6m / s Determine o módulo, a direção e o sentido do campo elétrico mais fraco capaz de trazer o próton uniformemente para o rep
Um elétron é liberado do repouso em um campo elétrico uniforme. O elétron acelera verticalmente de baixo para cima, percorrendo 4,5m nos primeiros 3μ s após ser libertado.Quais são o módulo, direção e
Campo elétrico da terra a terra possui uma carga elétrica líquida que produz um campo elétrico orientado para o centro da Terra com módulo de150N / C em Pontos próximos de sua superfície.Qual seria o
No Exercício 21.3, qual é a velocidade escalar do elétron quando ele emerge do campo?
Um próton é colocado em um campo elétrico uniforme de 2,75x10 3N / C , calcule:o módulo da força elétrica sofrida pelo próton;aceleração do prótona velocidade escalar do próton após 1μ s no campo, sup