Um raio de luz no ar incide sobre o prisma de ângulo reto mostrado na Figura 33.46. Esse raio possui dois comprimentos de onda diferentes. Quando emerge na face , ele se divide em dois raios diferentes com um ângulo de entre si. Calcule o índice de refração do prisma para cada um dos dois comprimentos de onda.
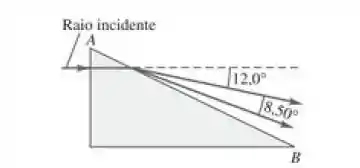
Passo 1
Opa! Vamos entender o que está acontecendo. Pra isso, vamos fazer um desenho e marcar alguns ângulos:
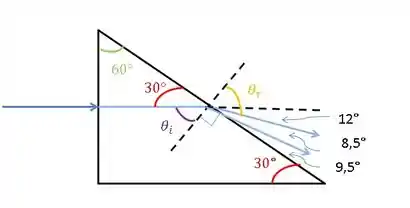
Aqui eu marquei o em relação ao raio que faz com a horizontal. Podemos usar o fato de que a normal é perpendicular à superfície, e teremos:
Agora que já sabemos o ângulo de refração, podemos usar a lei de snell:
Beleza! Agora temos que fazer a mesma brincadeira com os ângulos, só que com o outro raio. Vamos lá!
Passo 2
O , igual a gente tinha antes. Quem vai mudar é o Agora ele vai valer:
Aplicando a lei de snell:
Isso aí! Show de bola?!
Resposta
Ei, a resposta está no passo a passo :)