Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 33.Problemas - Ex. 58

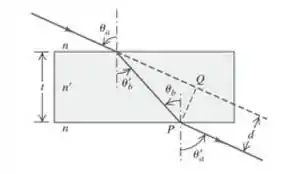
Um raio de luz propagando-se no ar incide com um ângulo θ a sobre a superfície superior de uma placa transparente (Figura 33.56), sendo suas duas superfícies planas e paralelas. a) Mostre que θ a = θ a ' . b) Prove que isso é verdade para qualquer número de placas paralelas diferentes. c) Demonstre que o deslocamento lateral   d do raio emergente é dado pela relação

d = t sen ⁡ θ a - θ b ' cos ⁡ θ b '

onde t é a espessura da placa. d) Um raio de luz incide com um ângulo de 66 ° sobre a superfície superior de uma placa de vidro com espessura de 2,40   c m e índice de refração igual a 1,80 . O meio dos dois lados da placa é o ar. Calcule o deslocamento lateral entre o raio emergente co raio incidente.

Passo 1

a)

Aplicando a lei de snell na interface cujos índices de refração são n   e n ' :

n sen ⁡ θ a = n ' sen ⁡ θ b '

Aplicando a lei de snell na interface cujos índices de refração são n '   e n :

n ' sen ⁡ θ b = n sen ⁡ θ a '

Pelas propriedades de retas paralelas cortadas por uma transversal, temos que θ b ' = θ b

Com isso, podemos igualar as equações:

n sen ⁡ θ a = n sen ⁡ θ a '

Então:

sen ⁡ θ a = sen ⁡ θ a '

Isso acontece quando:

θ a = θ a '

Show!

Passo 2

b)

conforme adicionamos mais interfaces entre o meio com índice de refração n , a lei de snell continua sendo válida interface à interface, então poderemos fazer um processo análogo ao que fizemos no item a, e ir substituindo e igualando as equações, de forma que ficaremos com os termos primeiro e ultimo.

n a sen ⁡ θ a = n b sen ⁡ θ b

n b sen ⁡ θ b = n c sen ⁡ θ c

E assim sucessivamente, até que

n z sen ⁡ θ z = n a sen ⁡ θ a '

E então:

n a sen ⁡ θ a = n a sen ⁡ θ a '

θ a = θ a '

Passo 3

c)

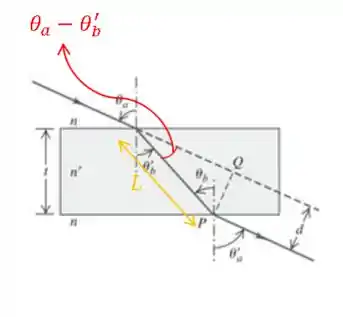
Olhando para o triângulo retângulo com a hipotenusa L , temos que L pode ser escrito como:

cos ⁡ θ b ' = t L

Então:

L = t cos ⁡ θ b '

Além disso, calculando o seno de θ a - θ b ' :

sen ⁡ θ a - θ b ' = d L

Então

d = L ⋅ sen ⁡ θ a - θ b '

Substituindo

d = t cos ⁡ θ b ' ⋅ sen ⁡ θ a - θ b '

Passo 4

d)

é só substituir os valores para acharmos o d .

d = t cos ⁡ θ b ' ⋅ sen ⁡ θ a - θ b '

d = 2,4 cos ⁡ θ b ' ⋅ sen ⁡ 66 ° - θ b '

Para encontrarmos o θ b ' , vamos aplicar a lei de snell:

n 1 sen ⁡ θ a = n 2 sen ⁡ θ b '

1 sen ⁡ 66 ° = 1,8 sen ⁡ θ b '

Então θ b ' = 30,5 ° . Com isso:

d = 2,4 cos ⁡ θ b ' ⋅ sen ⁡ 66 ° - θ b '

d = 2,4 cos ⁡ 30,5 ° ⋅ sen ⁡ 66 ° - 30,5 °

d = 1,62   c m  

Show!

Resposta

a) demonstração

b) demonstração

c) demonstração

d) d = 1,62   c m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Quando um tanque retangular de metal da Fig 33-46 está cheio até a borda de um líquido desconhecido, um observador O, com os olhos ao nível do alto do tanque , mal pode ver o vértice E. A figura mostr
Na Fig. 33-50a, um feixe luminoso que estava se propagando no meio 1 incide com um ângulo θ 140 ° na interface com o meio 2. Parte da luz penetra no meio 2 e parte dessa luz penetra no meio 3; todas a
Na Fig. 33-48a, um raio luminoso que estava se propagando na água incide com um ângulo θ 1 em outro meio, no qual parte da luz se refrata. O outro meio pode ser do tipo 1 ou do tipo 2; a Fig. 33-48b m
Na fig. 33-47a, um raio luminoso que estava se propagando em um certo meio indice com um ângulo θ 1 na água, onde parte da luz se refrata. O outro meio pode ser do tipo I ou do tipo 2; a fig. 33-47b m
Dispersão em um vidro de janela. Na Fig. 33-54, um feixe de luz branca incide com um ângulo θ = 50 ° em um vidro comum de janela (mostrado de perfil). Nesse tipo de vidro, o índice de refração da luz