Enunciado
Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 33.Problemas - Ex. 60
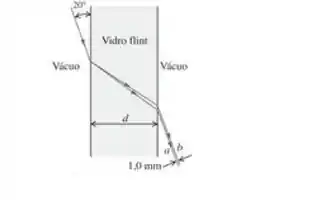
Um feixe estreito de luz incide normalmente sobre uma placa grande de vidro flint de silicato formando um ângulo de com a superficie da placa. Em virtude da dispersão, o feixe se subdivide formando um espectro, como indicado na Figura 33.58. O índice de refração do vidro flint em funçäo do comprimento de onda é mostrado no gráfico da Figura 33.18. a) Os raios a e b indicados na Figura 33.58 são as extremidades do espectro visível. Qual deles é o vemelho e qual é o violeta? Explique seu raciocínio. b) Para qual espessura da placa a largura do feixe do espectro deve ser iguai a ? (Veja o Problema 33.58.)
Passo 1
- Os comprimentos de onda do violeta e do vermelho no vácuo são e .
A relação entre comprimeto de onda e índice de refração é:
Como o , então , de fato, pela figura 33.18, temos que no vidro Flint e .
Sabemos que ao passar de um meio com , . Como , então , ou seja, b corresponde ao violeta e a corresponde ao vermelho.
Passo 2
b)Vamos por partes. Primeiro, vamos calcular a distância entre o raio vermelho e o feixe incidente, :
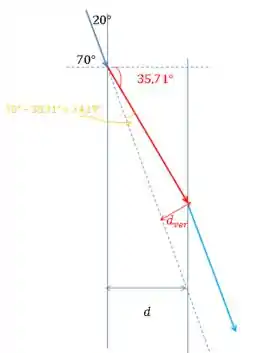
O ângulo de é encontrado a partir da lei de snell:
Show!
Agora, vamos olhar para um triângulos formados na figura.
Então
Beleza, guarda esse resultado aí.
Vamos olhar para outro triângulo:
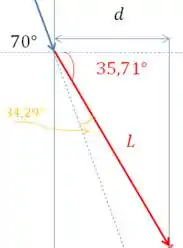
Então
Podemos igualar as duas equações, e teremos:
Show. Vamos fazer a mesma coisa, mas agora para o raio violeta.
Passo 3
Para o violeta:
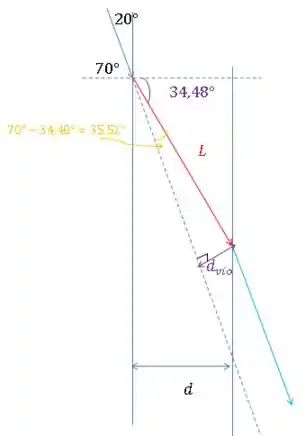
O ângulo é encontrado a partir da lei de snell.
Olhando para o triângulo, temos:
Olhando para esse triângulo:
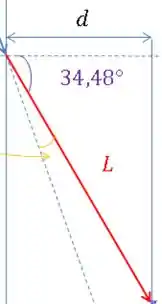
Igualando as duas equações:
Show!
Passo 4
A distância entre os dois feixes emergentes é a subtração de cada um em relação ao feixe incidente, ou seja:
Resposta
a) b corresponde ao violeta e a corresponde ao vermelho.
b)