Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 3.1 - Ex. 55
A rapidez de um avião voando em ar parado é de 250 km/h. Um vento sopra a 80km/h no sentido que aponta 60° a leste do norte. (a) Em qual sentido o avião deve apontar para viajar para o norte em relação ao solo? (b) Qual é a rapidez do avião em relação ao solo?
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão. O avião se move no ar, e o ar também está em movimento em relação ao solo. Como temos um objeto que se move sobre outro que se move, a gente tem uma questão de velocidade relativa.
A ideia é que o avião tem sua velocidade relativa ao vento (ao ar) de . E que o vento se move a em relação ao solo. Aí para saber o vetor velocidade do avião em relação ao solo a gente precisa fazer a soma vetorial dessas duas velocidades:
A partir dessa expressão a gente descobre a orientação de como ele pede no item (a) e o módulo de como ele pede no item (b).
Vamos lá analisar cada item!
Passo 2
a) Queremos saber a orientação da velocidade do avião em relação ao vento. Para achar orientações em velocidade relativa é bom desenhar a soma vetorial que a gente escreveu no passo 1.
A figura abaixo representa um esboço dos vetores atuantes na situação. é a velocidade do vento em relação ao solo, é a velocidade do avião em relação ao solo e é a velocidade do avião em relação ao vento.
O ângulo indica a direção que o avião deve seguir para que a resultante seja somente em direção ao norte.
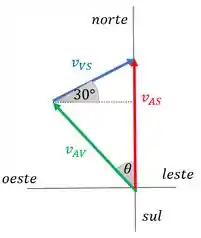
Ali temos o ângulo de no sentido de leste para norte que dá a orientação de . Ele é igual a orientação de no sentido a leste do norte (de norte para leste) que o enuciado descrever.
Passo 3
Percebe que temos dois triângulos retângulos na figura que compartilham esse segmento tracejado. Podemos então escrever o comprimento dele a partir de duas perspecitivas e igualar as expressões.
Para o triângulo de cima, temos:
Para o segundo triângulo:
Igualando essas duas expressões:
Como queremos , vamos isolar esse cara:
Esse ângulo está de norte para oeste (a oeste do norte).
Passo 4
b) A rapidez do avião em relação ao solo é o módulo da velocidade do avião em relação ao solo, ou seja, do vetor vermelho na nossa figura:
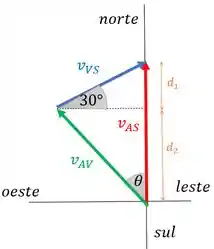
Então basicamente a gente precisa achar o comprimento dele. Por isso, vamos achar e e somar.
Olhando para o triângulo retângulo de cima, vamos ter:
E o triângulo de baixo nos dá:
Somando essas duas distâncias, vamos achar:
Substituindo os dados:
Resposta
(a oeste do norte)