Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 6.1 - Ex. 29
Uma extremidade de uma mola leve (constante k) é presa ao teto e a outra extremidade é presa a um objeto de massa m. A mola está frouxa e na vertical, inicialmente. Primeiro, você abaixa o objeto, vagarosamente, até urna posição de equilíbrio a uma distância h abaixo da posição inicial. Depois, você repete a experiência, mas agora largando o objeto, e o resultado é que ele cai uma distância H abaixo da posição inicial, até parar momentaneamente. (a) Mostre que h = mg/k, (b) Use o teorema do trabalho-energia cinética para mostrar que H = 2h. Tente você mesmo esta experiência.
Passo 1
Letra (a)
Cara, temos uma mola frouxa presa no teto. Aí prendemos uma massa na extremidade de baixo da mola.
Se você só prender e soltar, a massa cai e a mola fica oscilando por um tempo. Mas o que ele faz aqui é ir abaixando a massa aos poucos até a posição de equilíbrio. Aí nesse caso, ela vai ficar parada causando uma deformação na mola.
O que ele quer é a expressão de . Vamos fazer o diagrama de corpo livre da massa quando ela está paradinha em equilíbrio:
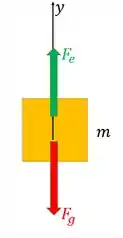
Temos a força gravitacional par abaixo e a força elástica tendendo a puxar a massa para cima (porque a mola quer voltar a posição inicial). Usando a segunda lei de Newton para , sabendo que (porque estamos em repouso):
Passo 2
E temos que e a força elástica é dada por :
Só que esse é a deformação da mola ao colocar a massa. E isso é a exatamente a altura que a mola é esticada:
Como queremos , vamos isolar:
Provamos o que ele pediu!
Passo 3
Letra (b)
Agora a massa foi presa a mola e foi largada depois. Então aqui houve aquela situação da oscilação que a gente falou no passo 1. A massa sai da posição inicial, cai e para momentaneamente a uma distância dessa posição (e depois fica oscilando).
Queremos saber a deformação da mola para esse caso.
Ele diz para usar o teorema trabalho-energia:
Isso diz que o trabalho total feito em uma partícula é igual à variação de energia cinética. A energia cinética é propocional a rapidez do objeto.
Como o objeto começa no repouso e o quando chega em ele fica no repouso de novo, temos que a energia cinética inicial e final no nosso caso são nulas. Logo o teorema fica:
Passo 4
Mas o trabalho total é a soma do trabalho que cada força faz sobre o objeto. No nosso caso é a soma do trabalho da força peso com o trabalho da mola:
O trabalho realizado pela força peso é dado pelo produto entre a força e o deslocamento, que nosso caso é , já que é constante:
Já o trabalho realizado pela mola é dado pela fórmulinha:
Sendo que a deformação da mola é e esse trabalho é negativo porque a força eslática está para cima (contrária ao movimento da massa que caiu).
Subsituindo tudo na expressão do teorema :
Corta uma vez:
E isola o H:
Lembrando que :
Resposta
Ver solução