Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 19.1 - Ex. 36
Recentemente, um antigo projeto de máquina térmica, conhecida como a máquina de Stirling, foi anunciado como uma maneira de se produzir potencia a partir da energia solar. O ciclo de uma máquina de Stirling é o seguinte: (1) compressão isotérmica do gás, (2) aquecimento do gás a volume constante, (3) expansão isotérmica do gás e (4) resfriamento do gás a volume constante. (a) Esboce os diagramas e para o ciclo de Stirling. (b) Determine a variação da entropia do gás, em cada etapa do ciclo e mostre que a soma dessas variações de entropia é igual a zero.
Passo 1
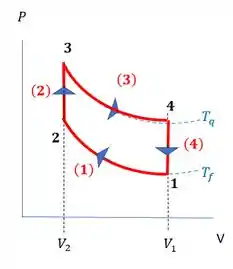
a) Ele quer os diagramas PV e ST, vamos começar pelo PV. Ele tem no eixo vertical a pressão e no horizontal o volume. Aí vemos como a pressão e o volume variam em cada processo.
- Em (1) temos a compressão isotémica do gás. Significa que o nosso gráfico nesse intervalo é uma curva com concavidade para cima (representando temperatura constante ), e que tem o sentido da direita para esquerda, porque o gás está diminuindo de volume.
- Em (2) o gás aquece a volume constante. Isso quer dizer que temos um segmento de reta na vertical, indicando que o volume não muda.
Ao aquecer o gás e manter seu volume, nós agitamos mais as moléculas que ficam confinadas, então a pressão aumenta. Por isso, o sentido desse processo no gráfico é de baixo para cima.
- Em (3) temos uma expansão isotérmica, novamente temos uma curva que representa a temperatura constante, mas agora que vale , e o sentido da curva é da esquerda para a direita, porque o volume do gás aumenta durante o processo.
- Para finalizar, em (4) temos um resfriamento a volume constante. Novamente vamos ter uma reta vertical, mas com o sentido de cima para baixo porque o resfriamento causa diminuição da pressão.
Com essas características, o gráfico vai ficar assim:
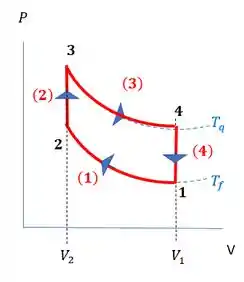
Passo 2
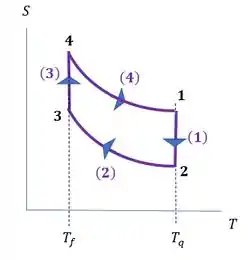
Agora vamos para o ST: Ele tem no eixo vertical a entropia e no horizontal a temperatura. Aí vemos como a entropia e a temperatura variam em cada processo.
- Em (1) temos a compressão isotémica do gás. Ou seja, a temperatura fica constante em , então vamos ter uma reta vertical, representando que a temperatura não mudou.
E que sentido tem essa reta? Vou te dar um bizu (que vamos ver a justificação ali na frente): se há uma compressão isotérmica, a variação de entropia do gás é negativa. Então nossa setinha fica para baixo.
- Em (2) o gás aquece a volume constante. Lembrando que a variação de entropia é proporcional a troca de calor, se ele aquece a volume constante, a variação de entropia é positiva, porque o gás está recebendo calor e não o está transformando em trabalho.
Aí nesse intervalo, teremos uma curva com concavidade para cima (parecida com a curva isotémica do PV), com sentido apontando de menor para maior (de baixo para cima).
- Em (3) temos uma expansão isotérmica. Ou seja, a temperatura fica constante em , então vamos ter uma reta vertical, representando que a temperatura não mudou. O sentido é de baixo para cima porque temos uma situação inversa ao processo (1).
Na expansão isotérmica, a entropia aumenta.
- Para finalizar, em (4) temos um resfriamento a volume constante. Novamente vamos ter uma curva, mas agora a setinha aponta para baixo, porque o calor está saindo do gás.
Com essas características, o gráfico vai ficar assim:
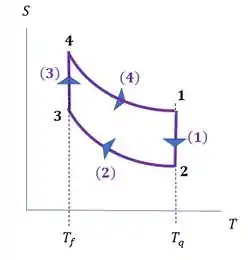
Passo 3
b) Agora vamos olhar a entropia de cada etapa.
Os processos e são isotérmicos, e para um processo isotérmico,
Então:
Mas lá do gráfico PV, a gente vê que e !
Passo 4
Os processos e são isovolumétricos, e para um processo isovolumétrico, podemos lembrar que
E podemos escrever
Então,
Mas percebe no diagrama ST que a temperatura final de 4-1 é e a inicial é , então:
Passo 5
Agora a gente soma todas pra achar a variação de entropia do ciclo!
Como a gente queria demonstrar!
Resposta
a)
