Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 12.1 - Ex. 13
Sua muleta é pressionada contra a calçada por uma força ao longo de sua própria direção, como na Figura 12-29. Esta força é equilibrada pela força normal e por uma força de atrito . (a) Mostre que, quando a força de atrito é máxima, o coeficiente de atrito está relacionado ao ângulo por . (b) Explique como este resultado se aplica às forças sobre o seu pé quando você não está usando uma muleta. (c) Explique por que é mais vantajoso dar passos curtos ao caminhar sobre pisos escorregadios.
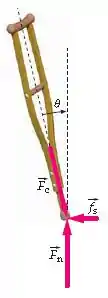
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Aplicando , temos:
Temos que:
Portanto:
Relacionando com a primeira equação, temos:
Passo 2
Item (b):
O resultado obtido é bem interessante. Pensa comigo... Se nós dermos grandes passadas tende a ser maior, portanto será maior, o que gera um maior atrito.
Passo 3
Item (c):
Se o piso é escorregadio, quer dizer que é pequeno, exigindo pequenas passadas para manter o equilíbrio. Se dermos longas passadas não haverá equilíbrio.
Resposta
Ei, a resposta está no passo a passo :)