Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Halliday - Vol 3- Ed: 4º - Capítulo 35.Problemas Adicionais - Ex. 43

Remova o capacitor do circuito da Fig. 31 - 7 e faça R = 200 Ω , L = 230 m H , f d = 60,0   H z e E m = 36,0   V . Determine o valor (a) de Z; (b) de ϕ ; (c) de I , (d) Desenhe um diagrama fasorial.

Passo 1

E aí galerinha, vamos destruir essa questão comigo? Vamos láaaa!

(a) Para R = 200 Ω e X L = ω d L = 2 π f d L = 2 π ( 60,0   H z ) 230 × 10 - 3 H = 86,7 Ω , a impedância é

Z = R 2 + X L 2 = ( 200 Ω ) 2 + ( 86,7 Ω ) 2 = 218 Ω

Passo 2

(b) De acordo com a Eq. 31-65, o ângulo de fase é

ϕ = t a n - 1 ⁡ X L - X C R = t a n - 1 ⁡ 86,7 Ω - 0 200 Ω = 23 , 4 ∘

Passo 3

(c) A amplitude da corrente é

I = ϵ m Z = 36,0 V 218 Ω = 0,165 A

Passo 4

(d) Vamos primeiro calcular as amplitudes das tensões entre os terminais dos componentes do circuito:

V R = I R = ( 0,165   A ) ( 200 Ω ) ≈ 33   V , V L = I X L = ( 0,165   A ) ( 86,7 Ω ) ≈ 14,3   V .

Como se trata de um circuito indutivo, ϵ m está adiantada em relação a I. O diagrama fasorial, desenhado em escala, aparece na figura a seguir.

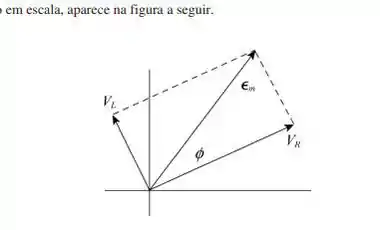
Opa, gostou da resolução? Responde Aí!

Resposta

a. 218 Ω

b. 23 , 4 ∘

c. 0,165 A

d. ϵ m está adiantada em relação a I.

Exercícios de Livros Relacionados

Uma fonte alternada com uma força eletromotriz de 6,00V e um ângulo de fase de 30 , 0 ∘ é ligada a um circuito RLC série. Quando a diferença de potencial entre os terminais do capacitor atinge o valor
Uma fonte de corrente alternada de frequência variável, um indutor de indutância L e um resistor de resistência R são ligados em série. A Fig. mostra a impedância Z do circuito em função da frequência
Na Fig. 31-7, faça R = 200 Ω , C = 70,0 μ F , L = 230 m H . f d = 60,0H z e E m = 36,0V . Determine o valor (a) de Z ; (b) de ϕ (c) de I. (d) Desenhe um diagrama fasorial.
Mostre que a potência dissipada na resistência R da Figé máxima quando R é igual à resistência r do gerador de corrente alternada. (Na discussāo do texto, supusemos tacitamente que r = 0 .)