Enunciado
Física - Moysés - Vol. 4 - Ed: 1º - Capítulo 2.Problemas - Ex. 10
Repita a dedução vista na Seç. 2.6 para um espelho esférico convexo, mostrando que se obtém a mesma relação distância-imagem (2.18), mas com , Mostre que a expressão (2.21) do aumento lateral também permanece válida nesse caso.
Passo 1
Opa! Vamos lá. Fiz um desenho análogo, mas considerando um espelho convexo. Olha aqui:
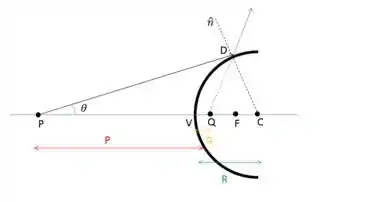
Marquei alguns pontos e ângulos que vamos precisar também.
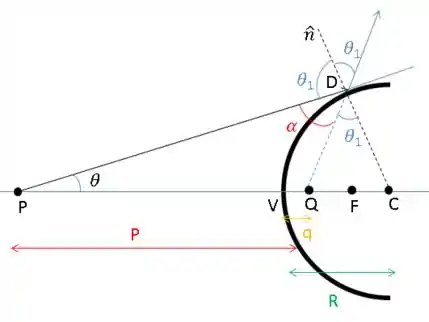
Usamos a lei de reflexão e ângulos opostos pelo vértice, ok?
Vamos usar a lei dos senos no triangulo :
Pela imagem vemos que
Então
Então
Pela regra da soma de arcos,
Ok. Guarda essa aí. Vamos fazer a mesma coisa para o triangulo .
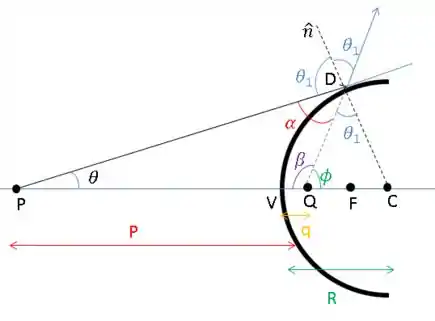
Mas
So que, para o triangulo a soma dos ângulos internos é
Então
Ma já vimos que
Então
Então
Então a lei dos senos fica:
Usando a soma de arcos:
Assim
Show!
Passo 2
Vamos recapitular o que achamos:
e
Daí, temos:
Usando a aproximação paraaxial, temos que .
E
Podemos escrever isso dessa forma:
Eaí,podemos substituir o que encontramos:
Vamos trabalhar com a igualdade, pois é assim que o livro fez para um espelho côncavo,ok?
Arrumando isso:
Mas, e ,então
Com e .
Assim
Como
Prontinho!!
Resposta
Ei, a resposta está no passo a passo :)