Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Moysés - Vol. 4 - Ed: 1º - Capítulo 7.Problemas - Ex. 6

Um pósitron de momento p → colide com um elétron em repouso, levando o par a aniquilar-se em dois fótons, cujas direções de propagação formam um ângulo θ   uma com a outra. Demonstre que a soma dos comprimentos de onda dos dois fótons é igual a   λ c ( 1 - cos ⁡ θ ) , onde   λ c é o comprimento de onda Compton do elétron (observe que o cálculo é semelhante ao do efeito Compton).

Passo 1

Primeiro de tudo, pósitron é a antiparticula do eletron, ele tem carga + e .

Então, temos um pósitron que colide com um eletron em repouso e isso gera dois fótons.

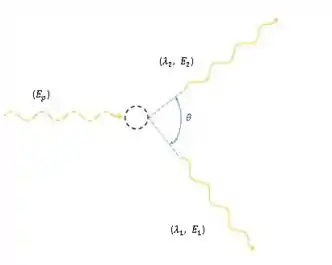
Vamos fazer a conservação da energia total relativística:

E p + m e c 2 = E 1 + E 2

E p = E 1 + E 2 - m e c 2

Onde m e c 2 é a energia de repouso do eletron.

Beleza. Mas a energia do pósitron se relaciona com seu momento por

E p 2 - p 2 c 2 = m e 2 c 4

E p 2 = m e 2 c 4 + p 2 c 2

Vamos elevar a primeira equaçãoao quadrado:

E p = E 1 + E 2 - m e c 2

E p 2 = E 1 + E 2 2 + m e 2 c 4 - 2 E 1 + E 2 m e c 2

Agora vamos igualar as expressões para E p 2 :

E 1 + E 2 2 + m e 2 c 4 - 2 E 1 + E 2 m e c 2 = m e 2 c 4 + p 2 c 2

E 1 + E 2 2 - 2 E 1 + E 2 m e c 2 = p 2 c 2

Mas,   p 2   nada mais é do que

p → ⋅ p → = E 1 c û 1 + E 2 c û 2 ⋅ E 1 c û 1 + E 2 c û 2

p 2 = E 1 c 2 + E 2 c 2 + 2 E 1 c E 2 c cos ⁡ θ

Então:

E 1 + E 2 2 - 2 E 1 + E 2 m e c 2 = p 2 c 2

E 1 + E 2 2 - 2 E 1 + E 2 m e c 2 = E 1 c 2 + E 2 c 2 + 2 E 1 c E 2 c cos ⁡ θ c 2

E 1 + E 2 2 - 2 E 1 + E 2 m e c 2 = E 1 2 + E 2 2 + 2 E 1 E 2 cos ⁡ θ

E 1 2 + E 2 2 + 2 E 1 E 2 - 2 E 1 + E 2 m e c 2 = E 1 2 + E 2 2 + 2 E 1 E 2 cos ⁡ θ

Simplificando...

2 E 1 E 2 - 2 E 1 + E 2 m e c 2 = 2 E 1 E 2 cos ⁡ θ

Então:

E 1 E 2 1 - cos ⁡ θ = E 1 + E 2 m e c 2

Mas

E = h c λ

Então

h c λ 1 h c λ 2 1 - cos ⁡ θ = h c λ 1 + h c λ 2 m e c 2

h c λ 1 h c λ 2 1 - cos ⁡ θ = λ 2 + λ 1 λ 1 λ 2 h c m e c 2

Arrumando:

h c m e c 2 1 - cos ⁡ θ = λ 2 + λ 1 λ 1 λ 2 λ 1 λ 2

h m e c 1 - cos ⁡ θ = λ 2 + λ 1

Mas λ c = h m e c .

λ c 1 - cos ⁡ θ = λ 2 + λ 1

Maravilha!

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um elétron de massa m e velocidade v “colide” com um fóton de raios gama cuja energia é h f 0 no referencial do laboratório. O fóton é espalhado na direção do movimento do elétron. Mostre que a energi
Mostre que ∆ E / E , a perda relativa de energia de um fóton em uma colisão com uma partícula de massa m , é dada por ∆ E E = h f ' m c 2 ( 1 - c o s ϕ ) Onde E é a energia do fóton incidente. f ' é a
Demonstre a Eq. 38-11, a equação usada para calcular o deslocamento de Compton, a partir das Eqs. 38-8, 38-9 e 38-10, eliminando ν e θ .
Considere um espalhamento Compton de um fóton que colide com um elétron que se move. Antes da colisão, o fóton possui comprimento de onda λ e está se deslocando no sentido + x e o elétron está se desl
A reação de fusão nuclear no centro do Sol produz fótons de raios gama com energia da ordem de 1M e V ( 10 6e V ) . Em contraste. O que vemos emanar da superfície do Sol são fótons de luz cujos compri