Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Moysés - Vol. 4 - Ed: 1º - Capítulo 2.Problemas - Ex. 13

Repita a dedução da Seç. 2.7 para uma superfície refratora esférica côncava, mostrando que a (2.28) permanece válida (com R < 0 ), bem como a última expressão na (2.32) para o aumento lateral.

Passo 1

Opa!

Vamos lá.

Vamos fazer um desenho marcando os pontos e distâncias e ângulos uteis:

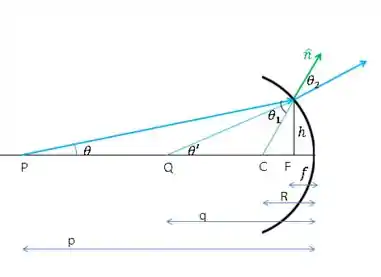
Agora, vamos usar a lei dos senos no triângulo   P C S :

R sen ⁡ θ = p - R sen ⁡ θ 1

sen ⁡ θ 1 sen ⁡ θ = p - R R

Fazendo o mesmo, para o triangulo   Q C S :

q - R sen ⁡ θ 2 = R sen ⁡ θ '

q - R R = sen ⁡ θ 2 sen ⁡ θ '

Fazendo a aproximação paraxial, temos;

sen ⁡ θ 2 sen ⁡ θ 1 = q - R p - R sen ⁡ θ ' sen ⁡ θ  

Se

tan ⁡ θ ' tan ⁡ θ ≅ sen ⁡ θ ' sen ⁡ θ = p q

Show!

Então

θ 2 θ 1 = q - R p - R p q

Usamos a lei de snell e a aproximação paraxial:

n 1 sen ⁡ θ 1 = n 2 sen ⁡ θ 2

sen ⁡ θ 2 sen ⁡ θ 1 ≈ θ 2 θ 1

E aí

n 1 n 2 = θ 2 θ 1

n 1 n 2 = q - R p - R p q

Arrumando isso:

p R - 1 q n 1 = n 2 q R - 1

n 1 p - n 2 q = - n 2 - n 1 R

Então é válida

n 1 p + n 2 q = n 2 - n 1 R

Com q < 0 e R < 0   .

Passo 2

Agora, vamos calcular o aumento lateral.

Podemos usar as propriedades dos foos e do raio central (que passa pelo centro C e não é desviado), juntamente com o caráter paraxial dos raios.

Desse modo:

m = - y ' y

m = - R + q p + R = - n 1 q n 2 p

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Espelhos esféricos. Um objeto O está sob o eixo central de um espelho esférico. Para cada problema a tabela mostra a distância do objeto p (em centímetros), o tipo de espelho e a distância (em centíme
Um espelho de barbear côncavo, com um raio de curvatura de 35,0c m , é posicionado de tal forma que a imagem (não invertida) do rosto de um homem é 2,5 maior que o riginal. A que distância o homem est
Uma xícara de chá é posicionada no eixo central de um espelho esférico. A ampliação lateral da xícara é +0,250 e a distância entre o espelho e o ponto focal é 2,00 cm. (a) Qual é a distância entre o e
Um feixe estreito, de raios paralelos, incide em uma esfera de vidro pela esquerda, na direção do centro da esfera. (A esfera se comporta como uma lente, mas certamente não é uma lente delgada.) Supon
Depois de se convencer (erroneamente) de que era impossível evitar a aberração cromática dos telescópios refratores, Isaac Newton inventou o telescópio refletor, mostrado esquematicamente na Fig. 34-5