Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 17.1 - Ex. 81
Para resolver esse problema, você utilizará uma planilha para estudar a distribuição das velocidades moleculares em um gás. A Figura 17-22 deve ajudá-lo a começar.
(a) Digite os valores para as constantes , e , como mostrado. Em seguida, na coluna A, insira valores de velocidade que variam de 0 a , em incrementos de . (Essa planilha será longa.) Na célula B7, insira a fórmula para a distribuição de velocidade fracionária de MaxwellBoltzmann. Essa fórmula contém os parâmetros , , e . Substitua A7 por , B $ 1 para R, B $ 2 para M e B $ 3 para T. Em seguida, use o comando FILL DOWN para inserir a fórmula nas células abaixo de B7. Crie um gráfico de f (v) versus v usando os dados nas colunas A e B.
(b) Explore como o gráfico muda à medida que aumenta e diminui a temperatura e descreva os resultados.
(c) Adicione uma terceira coluna na qual cada célula contém a soma cumulativa de todos os valores de f (v), multiplicada pelo tamanho do intervalo dv (que é igual a 1), nas linhas acima e incluindo a linha em questão. Qual é a interpretação física dos números nesta coluna?
(d) Para gás nitrogênio a 300 K, qual porcentagem das moléculas tem velocidades inferiores a 200 m / s? (e) Para gás nitrogênio a 300 K, qual porcentagem das moléculas tem velocidades superiores a 700 m / s?
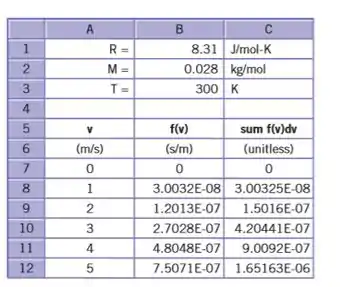
Passo 1
a) um grafico valido para é igual a esse:
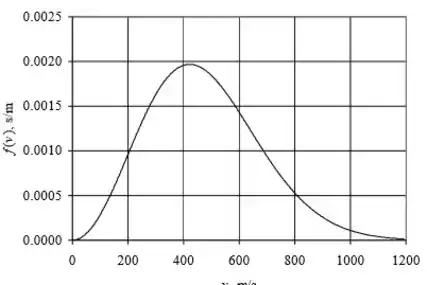
Passo 2
(b) À medida que a temperatura aumenta, a posição horizontal do pico se move para a direita na proporção da raiz quadrada da temperatura, enquanto a altura do pico cai pelo mesmo fator, preservando a área total sob o gráfico (que deve seja 1,0).
Passo 3
(c) Cada número na coluna C da planilha (mostrado em (a)) é aproximadamente igual à integral de f (v) de zero até o valor v correspondente. Essa integral representa a probabilidade de uma molécula ter uma velocidade menor ou igual a esse valor de v.
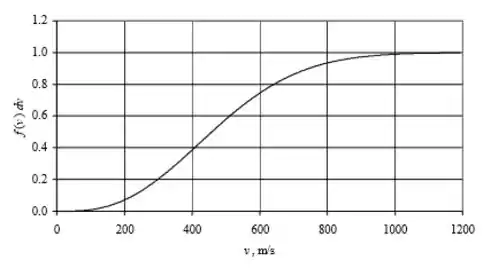
Passo 4
Observando a célula C207, descobrimos que a probabilidade (a 300 K) de uma molécula de nitrogênio com velocidade inferior a 200 m / s é 0706 .0, ou cerca de 7%. Observe que esse valor é consistente com o gráfico de mostrado imediatamente acima.
Passo 5
Olhando na célula C707, descobrimos que a probabilidade de uma molécula de nitrogênio ter uma velocidade menor que 700 m / s é de aproximadamente 0,862; portanto, a probabilidade de ela ter uma velocidade maior que isso seria 1 - 0,862 ou 138 .0, ou uma pouco menos de 14%.
Resposta
Ei, a resposta está no passo a passo :)