Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 4.Problemas - Ex. 39
Um salto vertical em pé. O jogador de basquete Darrel Griffth detém o recorde em salto vertical de . (Isso significa que ele se moveu de baixo para cima por , após seus pés deixarem o chão.) Griffth pesava .
- Qual é a velocidade dele, quando ele deixa o chão?
- Se o tempo da parte do salto imediatamente anterior a seus pés deixarem o chão foi de , qual foi sua aceleração média (módulo e direção) quando ele empurrava o corpo contra o chão?
- Desenhe o diagrama de corpo livre . Em termos das forças no diagrama, qual é a força resultante sobre ele? Use as leis de Newton e os resultados da parte para calcular a força média que ele aplicou sobre o solo.
Passo 1
Eaee, belezinha?? Bom... o enunciado nos diz que um jogador de basquete, de peso , se moveu de baixo para cima por .
Queremos encontrar a velocidade inicial quando ele deixa o chão.
Para isso, deveremos utilizar equações de MRUV para encontrarmos :
Onde é a velocidade final e é a aceleração da gravidade.
Além disso, também queremos encontrar a aceleração média em a partir do momento que ele salta.
Para isso, temos que saber que a aceleração média é dada por:
Por fim, devemos desenhar o diagrama de corpo livre para encontrar a força resultante que está atuando no atleta e calcular a força média que ele aplicou no solo no momento que saltou.
Passo 2
Sabendo que o deslocamento vertical foi , a velocidade final no alto do salto é zero e a aceleração da gravidade é podemos usar a equação de Toriccelli do MRUV para encontrar a velocidade inicial :
Dica : o sinal é porque a gravidade aponta na vertical para baixo.
Dica : se você não se lembra dessa equação não fique triste: corre lá na aba de movimento variado e tira todas tuas dúvidas!
Agora é só substituir:
Passo 3
Sabendo que aceleração média é:
Basta substituir os valores:
Passo 4
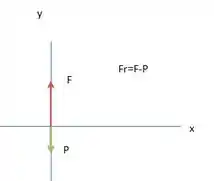
Sobre ele agem duas forças: a força peso (de módulo ) que aponta verticalmente para baixo e a força que o chão faz sobre ele (em reação à força que ele faz no solo) que aponta verticalmente para cima. O diagrama de forças para o corpo livre vai ser:
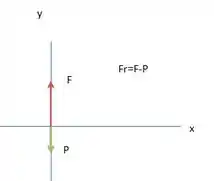
Como ele tem uma aceleração média que aponta para cima, sabemos que a força resultante vai ser para cima.
O módulo da força peso está representado em verde e o módulo da força , em vermelho.
A força resultante vai ser dada pela soma desses dois vetores:
Calculamos a aceleração no passo anterior e sabendo que a massa dele é:
Podemos calcular a força usando a segunda lei de Newton:
Resposta
