Dois adultos e uma criança querem empurrar uma caixa apoiada sobre rodas na direção do ponto marcado com na figura . Os dois adultos empurram com forças horizontais e como mostra a figura.
- Ache o módulo, a direção e o sentido da menor força que a criança deve exercer. Ignore os efeitos do atrito.
- Se a criança exercer a força mínima determinada pelo item , a caixa acelera a na direção . Qual é o peso da caixa?
Passo 1
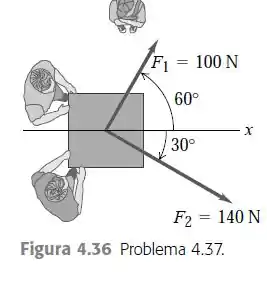
Eaee, belezinha?? Bom... o enunciado nos diz que dois adultos e uma criança querem empurrar uma caixa apoiada sobre rodas na direção do ponto marcado com :
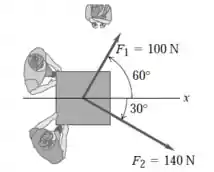
Os dois adultos empurram com forças horizontais e indicadas na figura.
Dado: ignore o atrito.
Queremos encontrar módulo, a direção e o sentido da menor força que a criança deve exercer.
Para isso, devemos fazer um diagrama de corpo livre a fim de analisar as componentes das forças!!
Depois que encontrarmos a força, o enunciado nos pede para calcularmos o peso da caixa dado que ela acelera a .
Para isso, devemos utilizar a segunda Lei de Newton:
Onde a força resultante sobre um corpo é dada pelo produto de sua massa pela aceleração .
Agora bora aplicar!! 😉
Passo 2
a) A gente quer saber que força mínima deve ser aplicada pela criança para que eles possam mover a caixa somente na horizontal.
Vamos fazer um desenho pra melhor representar a situação sem a força da criança.
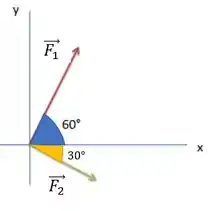
Os módulos das forças e (realizadas pelos dois adultos) estão representados em vermelho e verde respectivamente.
Para a gente movimentar essa caixa só no sentido de , precisamos que não haja movimento em . Ou seja, que haja equilíbrio de forças nesse eixo.
Se quisermos adicionar uma força (realizada pela criança) que seja a menor possível, então queremos manter a condição de que na direção vertical não há movimento.
Passo 3
Sendo assim, a soma de todas componentes verticais deve ser zero. As componentes verticais das forças e são:
A componente de fica negativa porque ela aponta para a parte negativa de .
E quando adicionarmos uma força associada a criança, temos que manter tudo em equilíbrio:
Substituindo os valores temos:
E a componente horizontal deve ser nula, porque aí teremos que essa força só tem componente nesse eixo e o seu módulo é esse que achamos.
Se houvesse algum valor para a componente em , o módulo da força aumentaria (não seria o mínimo que queremos).
Assim a força mínima que a criança deve fazer é:
Passo 4
b) Agora o problema pergunta qual o peso da caixa. Relembrando como se calcula a força peso temos:
Precisamos da massa dessa caixa! Mas pera aí, isso não foi dado no exercício!
Mas saca só, o problema nos diz o valor da aceleração que a caixa está sendo submetida!
Daí lembrando-se da segunda lei de Newton tem que a soma de todas as forças sobre um sistema vai ser proporcional ao produto da massa pela aceleração:
Já temos a aceleração, e sabemos que ela é na direção de , então agora vamos dar uma olhadinha novamente no desenho e ver qual é a força resultante.
Passo 5
Temos a ação dos dois adultos e podemos, assim como fizemos no item anterior, decompor para achar a componente horizontal.
As componentes horizontais das forças são:
E a força resultante sobre a caixa vai ser a soma dessas duas componentes (lembrando que a força com que a criança empurra a caixa é apenas na direção vertical, não conta na resultante de forças na horizontal):
Passo 6
Show! Agora que sabemos a força resultante e a aceleração, podemos determinar a massa:
E assim podemos finalmente calcular o peso: