Enunciado
Física - Young and Freedman - Vol 3- Ed: 14º - Capítulo 21.Exercícios - Ex. 86
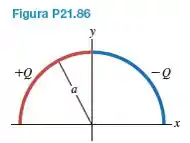
Um semicírculo de raio a se encontra no primeiro e no segundo quadrantes, com seu centro de curvatura na origem. A carga positiva está distribuída uniformemente ao longo da metade do lado esquerdo do semicírculo, e a carga negativa está distribuída uniformemente ao longo da metade do lado direito do semicírculo (Figura P21.86). Determine o módulo, a direção e o sentido do campo elétrico resultante na origem produzido por essa distribuição de cargas.
Passo 1
Olá, tudo bem? Vou ajudar você aqui!
Vou analisar primeiro a simetria desse caso. A parte positiva do fio vai produzir um campo elétrico para fora, no sentido do quarto quadrante. Já a parte negativa, vai produzir um campo elétrico para dentro, no sentido do primeiro quadrante. Saca só nesse desenho:
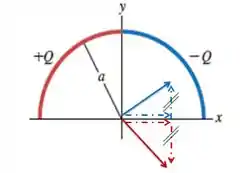As componentes verticais de cada um desses pedacinhos de fio vão ser canceladas e no fim vamos ter apenas duas componentes horizontais. O campo resultante então será horizontal para a direita.
Passo 2
E quanto ao módulo dele? Bom, calculamos no exercício o campo devido à quarta parte de um fio carregado com uma carga e esse módulo é:
E aqui vou reutilizar esse resultado! Já que tanto o fio vermelho quanto o fio azul produzem esse mesmo valor de campo. Mas atenção, devemos somar as duas contribuições, já que temos duas quartas partes de fio, ok?
Assim o campo na origem é: