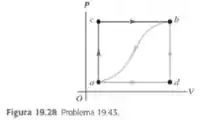
Quando um sistema vai do estado até o estado (Figura 19.28) pelo caminho , um calor igual a flui para o interior do sistema, e um trabalho de é realizado pelo sistema. a) Qual é o calor que flui para o interior do sistema pelo caminho , sabendo que o trabalho realizado pelo sistema é igual a ? b) Quando o sistema retorna de para pelo caminho encurvado, o valor absoluto do trbalho realizado pelo sistema é igual a . O sistema absorve ou libera calor? Qual é a quantidade desse calor? c) Sabendo que e , calcule os calores absorvidos nos processos e .

Vamos então calcular usando as informações do caminho :

E usar o valor que encontramos para calcular o calor que flui para o sistema no caminho :

O trabalho já é dado no enunciado, isolamos :

E substituímos os valores:

b) Como agora o sistema vai de para , a variação de energia interna muda de sinal em relação ao que calculamos antes:

Além disso, como o volume diminui, então o trabalho do gás é negativo:

E usando a primeira lei da termodinâmica:

Ficamos com o seguinte calor:

Como o sinal é negativo, o sistema libera calor.

c) Beleza, todo o trabalho do caminho está na parte , porque em o volume não varia, e o gás não trabalha, assim:

A primeira lei da termodinâmica fica, considerando e dados na letra (c):

Isolando e substituindo os valores:

Agora para o calor no caminho , basta pegarmos o calor do caminho e subtrairmos o que achamos em , que será o calor só do processo :

Substituindo valores: