Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 20.1 - Ex. 19
Suponha que de um gás monoatômico ideal inicialmente à pressão e ocupando um volume seja submetido sucessivamente a dois processos: uma expansão isotérmica até um volume e um aumento de pressão a volume constante até uma pressão .
Qual é o valor de
para o processo e
para o processo ?
Qual é o valor de
para o processo e
para o processo ?
Para o processo completo, qual é o valor
de
e de ?
O gás retorna ao estado inicial e é levado ao mesmo estado final, mas desta vez através dos seguintes processos sucessivos: uma compressão isotérmica até a pressão de e um aumento de volume até um volume de à pressão constante.
Qual é o valor de
para o processo e
para o processo ?
Qual é o valor de
para o processo e
para o processo ?
Para o processo completo, qual é o valor
de e
de ?
Passo 1
Olá pessoal, essa é uma questão bem longa. Então toma fôlego aí e vem comigo resolver!
Antes de começar vou colocar aqui duas informações que vamos usar sempre: e . Bora começar?
Vou também fazer um desenho para as letras pra ficar melhor de entender:
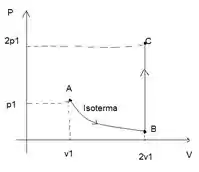
Analisando o primeiro gráfico, tiramos as seguintes informações dos estados :
Feito isso, a primeira coisa a fazer é analisar o processo . Ele é isotérmico, então . Então da primeira lei temos:
Agora da lei geral dos gases temos:
Assim podemos substituir a temperatura ali em cima:
Sendo assim a razão é:
Passo 2
Para determinar a mesma razão, mas agora olhando pro processo dois ( do gráfico): temos que ele é isocórico, ou seja com . Então o calor vai ser dado por:
Mas sabemos que , agora precisamos determinar a temperatura .
Pela lei dos gases, comparando os estados e do gráfico, temos:
Daqui tiramos que: .
Já o é dado por
Agora podemos volta ao calor :
Agora o valor da razão é:
Passo 3
Em um processo isotérmico, então , assim, copiando o resultado do Passo , no qual , então a razão que o problema pede é:
Passo 4
Já para o processo é diferente, pois ele é isocórico! E isso quer dizer que o trabalho é zero! Então a razão é zero.
Passo 5
Agora queremos saber a variação da energia interna para o processo completo. Sendo assim, a variação da energia interna total vai ser a soma das variações de cada processo. Como no processo (pois é isotérmico), então a variação de energia interna total vai ser só dado pelo processo .
Sabendo que é um processo isocórico, então e da primeira lei temos:
Agora dá uma espiada no Passo . Já calculamos esse calor! Assim teremos:
E a razão é:
Passo 6
A a variação de entropia? Bom, ela devemos também separar nos dois processos:
- Isotérmico:
- Isocórico (lembrando que e ):
Como já calculamos o calor desse processo
Como o processo é isovolumétrico ()
E a variação de entropia total vai ser a soma:
Passo 7
Agora vamos analisar o segundo gráfico, que vai servir pras letras :
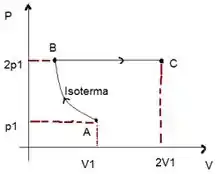
Analisando o gráfico, tiramos as seguintes informações dos estados :
Agora vamos analisar o primeiro processo: ele é isotérmico, então . Então da primeira lei temos:
Agora da lei geral dos gases temos:
Assim:
E também:
Assim podemos substituir a temperatura ali em cima:
Sendo assim a razão é:
Passo 8
O processo é isobárico, sendo assim:
Pela lei dos gases, comparando os estados e do gráfico, temos:
Assim e como :
Sendo assim a razão é:
Passo 9
Em um processo isotérmico, então , assim, copiando o resultado dos Passos , no qual , então a razão que o problema pede é:
Passo 10
Agora a mesma razão, mas agora para o processo : isobárico. O trabalho é bem tranquilo:
Todos esses dados temos lááá no passo , dá uma espiada lá e volta aqui:
E a razão fica:
Passo 11
Vamos calcular a variação da energia interna?
Bom, já estamos carecas de saber que para um processo isotérmico , sendo assim não temos contribuição do processo . O processo é isobárico, então a variação total da energia interna vai ser:
Se dividirmos por dos dois lados vamos ter:
UFA! VAMOS PRA ÚLTIMA! Toma fôlego e vem comigo!
Passo 12
E a variação de entropia? Bom, ela devemos também separar nos dois processos:
- Isotérmico:
- Isocórico (lembrando que e ):
Como já calculamos esse calor
Como o processo é isobárico ()
Que é a mesma reposta do passo 6! Até por que os estados inicial e final dos dois processos são iguais. Você podia responder assim, mas não custa nada dar uma treinada a mais não é mesmo?