Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 9.Problemas - Ex. 87

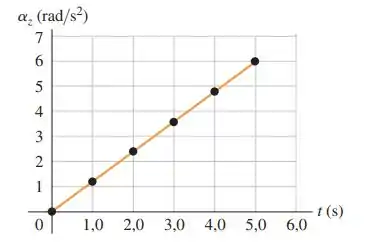
Uma técnica está testando um motor de velocidade variável, controlado por computador. Ela prende um disco fino ao eixo do motor, com o eixo no centro do disco. Este parte do repouso e sensores ligados ao eixo do motor medem a aceleração angular α z do eixo em função do tempo. Os resultados de um teste aparecem na Figura P 9.87 . (a) Quantas rotações o disco terá feito nos primeiros 5,0   s ? Você pode usar a Equação 9.11 ? Explique. Qual é a velocidade angular, em r a d / s , do disco (b) em t = 5,0   s ; (c) quando ele tiver girado por 2,00 rotações?

Passo 1

Fala, galera! Beleza? Vamos resolver essa questão!

O enunciado pediu pra gente determinar quantas rotações o disco terá feito nos primeiros 5,0   s , a velocidade angular do disco em t = 5,0   s e quando ele tiver girado por 2,00 rotações.

Como a aceleração angular não é constante, a Eq. ( 9.11 ) não pode ser usada, então devemos usar:

α 2 = d ω 2 d t

E

  ω z = d θ d t

E integrar para encontrar o ângulo.

Vamos lá!

Passo 2

O gráfico passa pela origem e tem uma inclinação positiva constante de 6 / 5 r a d / s 3 , então a equação para α z é:

α z = 1 , 2   r a d / s 3 t

Usando α z = d ω z d t , temos:

ω z = ω 0 z + ∫ 0 t   α z d t

ω z = 0 + ∫ 0 t   1 , 2 r a d s 3 t d t

ω z = 0 , 60   r a d s 3 t 2

Agora, devemos usar a 2 = d θ d t e integrar novamente para obter o ângulo:

θ 2 - θ 1 = ∫ 0 t   ω 2 d t

θ 2 - θ 1 = ∫ 0 t   0 , 60 r a d s 3 t 2 d t

Integrando, temos:

θ 2 - θ 1 = 0 , 20   r a d s 3 t 3

E substituindo os valores, obtemos:

θ 2 - θ 1 = 0 , 20   r a d s 3 ( 5 , 0   s ) 3

θ 2 - θ 1 = 25   r a d

Passo 3

b) O resultado da nossa primeira integração nos dá:

ω z = 0.60 r a d s 3 ( 5 , 0 s ) 2

ω z = 15   r a d / s

Passo 4

c) O resultado da nossa segunda integração nos dá

4 π r a d = 0 , 20   r a d s 3 t 3 ,  

t = 3 , 98   s

ω z = 0 , 60 r a d s 3 ( 3 , 98 s ) 2

ω z = 9,48   r a d / s

Valeu, galera! Até a próxima! 😉

Resposta

  1. 25   r a d
  2. 15   r a d s
  3. 9 , 48   r a d s
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os ciclos de rotação de uma máquina de lavar possuem duas velocidade angulares, 423 rev/min e 640 rev/min. O diâmetro interno do tambor é igual a 0.470mQual é a razão entre a força radial máxima sobre
A roda de uma olaria gira com aceleração angular constante igual a 2.25 rad/s^2. Depois de 4.00s, o ângulo descrito pela roda era de 60.0 rad. Qual era a velocidade angular da roda no início do interv
Um volante leva 4.00s para girar através de um ângulo de 162 rad. Sua velocidade angular nesse instante final é igual a 108 rad/s. Calcule a) a velocidade angular no início desse intervalo de 4.00s; b
A lâmina de uma serra circular de diâmetro igual a 0.200 m começa a girar a partir do repouso. Em 6.0 s ela se acelera com velocidade angular constante até uma velocidade angular igual a 140 rad/s. Ca
Deduza uma expressão para um movimento com aceleração angular constante que forneça θ - θ 0 em função de omega, de alpha e de t (não use omega_zero na equação).Para t = 8.0s, uma engrenagem gira em to