Uma halterofilista de 72 kg realizando exercícios de levantamento para os braços segura um peso de 7,50 kg. Seu braço se movimenta em torno do cotovelo, começando a 40,0° abaixo da horizontal (Figura P11.54). Medições biométricas mostraram que, juntos, antebraços e mãos compõem 6,00% do peso de uma pessoa. Como o braço superior é mantido na vertical, o músculo bíceps sempre atua verticalmente e está ligado aos ossos do antebraço 5,50 cm a partir do cotovelo. O centro de massa da combinação antebraço-mão dessa pessoa está a 16,0 cm do cotovelo, ao longo dos ossos do antebraço, e ela segura o peso a 38,0 cm de seu cotovelo. (a) Desenhe um diagrama do corpo livre do antebraço. (b) Que força o bíceps exerce sobre o antebraço? (c) Determine o módulo, a direção e o sentido da força que o cotovelo exerce sobre o antebraço. (d) À medida que a halterofilista levanta seu braço em direção a uma posição horizontal, a força no bíceps aumenta, diminui ou permanece igual? Por quê?
Passo 1
E aii galera, vamos fazer mais uma questão?
Letra a:
O diagrama de corpo livre é mostrado abaixo, onde a força de tensão é para cima enquanto o peso do braço, o peso da massa e a força vertical são para baixo
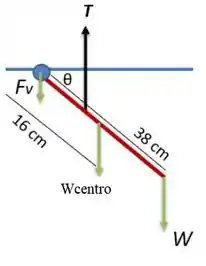
Passo 2
Letra b:
A força que o músculo bíceps exerce no antebraço é a tensão T. O peso está em estado de equilíbrio, então a soma do torque em torno do eixo é zero.
Agora, conectamos os valores para os parâmetros dados na última equação para obter T.
Passo 3
Letra c:
A articulação do cotovelo exerce uma força vertical no antebraço . Esta força é na direção oposta à tensão e igual ao peso do centro, o peso da massa. Então, podemos obter uma fórmula para esta força:
Passo 4
Letra d:
A força que o músculo bíceps exerce no antebraço é a tensão T, e encontramos uma fórmula para a tensão na parte (b):
Como mostrado, a tensão é independente do ângulo , então a força será a mesma enquanto o halterofilista levanta o braço em direção à posição horizontal.
Resposta
- Ver diagrama
- A força será a mesma quando o halterofilista levanta o braço em direção à posição horizontal.