Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 10.Problemas - Ex. 59
A Figura P10.59 ilustra uma máquina de Atwood. Ache as acelerações lineares dos blocos A e B, a aceleração angular da roda C e a tensão em cada lado da corda se não houver deslizamento entre a corda e a superfície da roda. Considere que as massas dos blocos A e B sejam 4,00 kg e 2,00 kg, respectivamente, o momento de inércia da roda em torno do seu eixo seja 0,220 kg m² e o raio da roda seja 0,120 m.
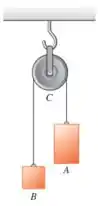
Passo 1
E aiiiiiiiii galera, tudo bom com vocês?
Vamos fazer mais uma questão!!
Bom... o enunciado dá a seguinte figura:
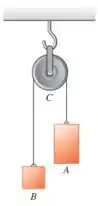
Onde a massa do corpo e do corpo são, respectivamente, e . Além disso, o momento de inércia da roda em torno do seu eixo é e o raio da roda é .
Queremos encontrar as acelerações lineares dos blocos A e B, a aceleração angular da roda C e a tensão em cada lado da corda se não houver deslizamento entre a corda e a superfície da roda.
Para resolver isso, vamos utilizar o princípio de conservação de energia!!
Passo 2
Primeiramente vamos expressar a energia potencial como função do tempo:
Onde é a massa do corpo A, é a massa do corpo , é a aceleração da gravidade, é a aceleração dos blocos (que é igual pois os corpos estão conectados) e é o tempo.
Já para a energia cinética , temos:
Onde é o momento de inércia e é o raio.
Em seguida, vamos aplicar o princípio de conservação de energia, cancelando os termos do tempo e isolando a aceleração , temos:
Passo 3
Assim, substituindo os valores para encontrar a aceleração, temos:
E, para a aceleração angular , temos:
Passo 4
Com isso, podemos calcular as nossas tensões .
Aplicando a Segunda Lei de Newton para o bloco , temos:
Passo 5
E, para o bloco :