Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 29.1 - Ex. 58

A tensao do gerador na Figura 29-40edada por S = ( 100  V)  c o s ⁡ ( 2 π f t )  .  a)Para cada ramo,qual e a corrente de pico e qual e a fase da corrente relativa a fase da tensao do gerador?(b)Na frequencia de ressonancia nao ha corrente no gerador.Qual e a frequência angular na ressonancia?(c)Na frequencia de ressonancia,determine a corrente no indutor e a corrente no capacitor.Expresse seus resultados como funcao do tempo.(d)Desenhe um diagrama de fasores mostrando os fasores para a tensao aplicada,a corrente no gerador, a corrente no capacitor e a corrente no indutor para o caso onde a frequencia emaior que a de ressonancia.

Passo 1

Oi oi gente, como vocês estão?

Vamos fazer uma questão passo a passo?

Vamos! Vem comigo.

Sabemos que a corrente conduz a tensão através de um capacitor e atrasa a tensão de um indutor. Podemos usar I L ,  pico  = ε pico X L   e   I C ,  pico  = ε pico  / X C para encontrar as amplitudes dessas correntes. A corrente no gerador desaparecerá em condições de ressonância, ou seja, quando I l = I c . Para encontrar as correntes no indutor e no capacitor na ressonância, podemos usar a diferença de potencial comum entre eles e suas reatâncias juntamente com nosso conhecimento das relações de fase mencionadas acima.

Passo 2

Letra a:

Expresse as amplitudes das correntes através do indutor e do capacitor:

I L ,  pico  = ε pico  X L = ε pico 2 π g

E

I C ,  pico  = ε pico X C = ε pico 1 2 π f C = 2 π f C ε pico

Substitua os valores numéricos para obter:

I L ,  pico  = 100 V ( 4.00 H ) 2 π f = 25.0 V / H 2 π f ,  atrasado de   ε  em   90 ∘

E

I C ,  pico  = 25.0 μ F 100 V ω = ( 2.50 m V ⋅ F ) 2 π f  , adiantado de   ε  em  90 ∘

Passo 3

Letra b:

Expresse a condição de que I = 0 :

I L = I C  or  ε ω L = ε 1 ω C = ω C E

Resolva para ω para obter:

ω = 1 L C

Substitua os valores numéricos e avalie ω :

ω = 1 ( 4.00 H ) ( 25.0 μ F ) = 100 r a d / s

Passo 4

Letra c:

Expresse a corrente no indutor em ω = ω 0 :

I L = 25.0 V H 100 s - 1 cos ⁡ ω t - π 2 = 250 m A cos ⁡ ω t - π 2   o n d e   ω = 100 r a d / s

Expresse a corrente no capacitor em   ω = ω 0 :

I c = ( 2.50 m V ⋅ F ) 100 s - 1 c o s ⁡ ω t + π 2

= - ( 250 m A ) c o s ⁡ ω t + π 2

onde  ω = 100 r a d / s

Passo 5

Letra d:

O diagrama fasorial para o caso em que a reatância indutiva é maior do que a reatância capacitiva é mostrado à direita

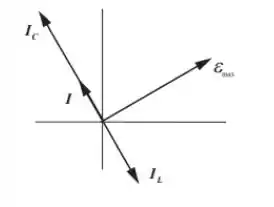
Resposta

  1. I L ,  pico  = 100 V 4.00 H 2 π f = 25.0 V H 2 π f ,  atrasado de   ε  em   90 ∘

    2. I C ,  pico  = 25.0 μ F 100 V ω = ( 2.50 m V ⋅ F ) 2 π f  , adiantado de   ε  em  90 ∘

  2. ω = 1 ( 4.00 H ) ( 25.0 μ F ) = 100 r a d / s
  3. = - ( 250 m A ) c o s ⁡ ω t + π 2
  4. Ver resolução
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A figura 31-36 mostra um “autotrasnformador”. Nesse dispositivo uma bobina com três terminais é enrolada em um núcleo de ferro. Entre os terminais T 1 e T 2 existem 200 espiras e entre os terminais T
Um gerador de CA alimenta uam carga resistiva em uma fábrica distante através de uma linha de transmissão de dois cabos. Na fábrica, um transformador abaixador de tensão reduz a tensão do valor de tra
Quando a força eletromotriz do gerador do Exemplo 31.07 é máxima, qual é a tensão (a) do gerador, (b) do resistor, (c) do capacitor e (d) do indutor? Some as tensões, com os sinais apropriados, para m
28 - Um circuito RLC em série é conectado a uma fonte de CA de 120 H z cuja tensão eficaz é dada por V q m = 80,0V . O circuito possui resistência de 75 Ω e uma impedância igual a 105 Ω para essa freq
38 - Um transformador para elevar a tensão. Um transformador conectado a uma fonte CA de 120 V (valor eficaz) deve fornecer 13000 V (valor eficaz) a um anúncio de neônio. Para prevenir o risco de choq