Um trem de metrô parte do repouso em uma estação e acelera com uma taxa constante de durante . Ele viaja com velocidade constante durante e reduz a velocidade com uma taxa constante de até parar na estação seguinte. Calcule a distância total percorrida.
Passo 1
Opa, bora resolver esse problema! Aqui temos um trem indo de um ponto ao outro e o enunciado nos dá as seguintes informações sobre a velocidade e sua aceleração:
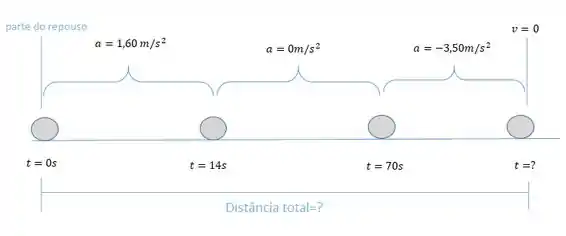
Vamos dividir em partes:
1º parte: o trem sai do respouso acelerando até uma taxa constante;
2º parte: o trem mantém uma velocidade constante;
3º parte: o trem desacelera até o repouso.
Não sabemos a distância total e é isso que vamos calcular!
Passo 2
Agora vamos analisar cada parte:
Na 1º parte, o espaço percorrido 14s e uma aceleração contante, pode ser calculado pela formulinha do “sorvetão”:
Substituindo os valores:
E descobrimos sua velocidade com a seguinte formulinha:
Passo 3
Na 2º parte temos que a aceleração é constante,
O tempo é:
Então nossa formula,
Fica assim:
Passo 4
No 3º trecho temos uma desaceleração até que o trem pare,o que significa que temos uma aceleração negativa:
Para descobrir quanto tempo ele leva para chegar ao repouso, sabemos que:
Então, temos que:
Agora vamos calcular o espaço percorrido:
E a distancia total percorrida é a soma dos 3 deslocalmentos: