Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 21.1 - Ex. 30
Três cargas puntiformes, cada uma com magnitude igual a , estão em três dos vértices de um quadrado de aresta igual a . As duas cargas puntiformes nos vértices opostos são positivas e a terceira carga é negativa. Determine a força exercida por estas cargas puntiformes em uma quarta carga puntiforme, , que está no quarto vértice.
Passo 1
Veja o esquema a seguir:
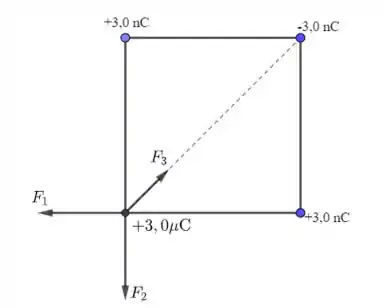
Vamos calcular cada uma dessas forças:
Da mesma forma, temos que . Como e são perpendiculares, temos que
e essa força está na direção da diagonal do quadrado. Além disso,
Sendo assim, a força resultante é:
Resposta
O módulo da força resultante é e aponta na diagonal do quadrado.
Exercícios de Livros Relacionados
Um nêutron é composto por um quark "up", com uma carga de + 2 e / 3 , e dois quarks "down", cada um com uma carga de - e / 3 . Se os dois quarks "down" estão separados por uma distância de 2,6 × 10 -
(a) Explique o que acontece com as esferas do Problema 42 se uma delas é descarregada (ligando, por exemplo, momentaneamente a esfera à terra). (b) Determine a nova distância de equilíbrio x, usando o
A que distância devem ser colocados dois prótons para que o módulo da força eletrostática que um exerce sobre o outro seja igual à força gravitacional a que um dos prótons está submetido na superfície
Na Fig. 21-39, quatro partículas são mantidas fixas no eixo x, separadas por uma distância d=2,00c m . As cargas das partículas são q 1=+ 2 e , q 2=- e ,q 3=+ e e q 4=+ 4 e , onde e =1,60 × 10 - 19C .
Na Fig. 21-22, as partículas 1 e 2 são mantidas fixas. Se a força eletrostática total exercida sobre a partícula 3 é zero e L 23=2,00 L 12 , qual é o valor da razão q 1/ q 2 ?