Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 27.1 - Ex. 38

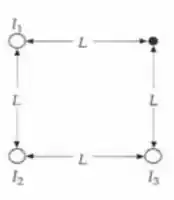
Três fios longos e paralelos estão nos vértices de um quadrado, como mostrado na Figura 27-54. Cada fio conduz uma corrente I. Determine o campo magnético no vértice não ocupado do quadrado quando

a) Todas as correntes estão entrando na página.

b) I 1   e   I 3 estão para dentro da página e I 2 está saindo.

c) I 1   e   I 2 estão para dentro da página e I 3 está saindo. Suas respostas devem estar em termos de I e L.

Passo 1

a)

Meus grandes gênios!

Vamos considerar que o campo magnético resultante é dado por:

B → = B 1 → + B 2 → + B 3 →

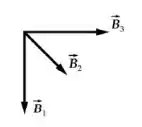
Portanto:

B 1 → = - μ 0 4 π 2 I L ∙ j

B 2 → = μ 0 4 π 2 I L 2 ∙ cos ⁡ 45 ° ∙ i - j = μ 0 4 π 2 I 2 L ∙ ( i - j )

B 3 → = μ 0 4 π 2 I L ∙ i

Com isso:

B → = B 1 → + B 2 → + B 3 → = - μ 0 4 π 2 I L ∙ j + μ 0 4 π 2 I 2 L ∙ i - j + μ 0 4 π 2 I L ∙ i

Resolvendo, encontraremos:

B → = 3 μ 0 4 π I L i - j

Passo 2

b)

Vamos considerar que o campo magnético resultante é dado por:

B → = B 1 → + B 2 → + B 3 →

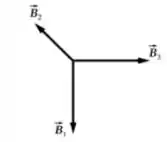
Portanto:

B 1 → = - μ 0 4 π 2 I L ∙ j

B 2 → = μ 0 4 π 2 I L 2 ∙ cos ⁡ 45 ° ∙ i - j = μ 0 4 π 2 I 2 L ∙ ( - i + j )

B 3 → = μ 0 4 π 2 I L ∙ i

Com isso:

B → = B 1 → + B 2 → + B 3 → = - μ 0 4 π 2 I L ∙ j + μ 0 4 π 2 I 2 L ∙ - i + j + μ 0 4 π 2 I L ∙ i

Resolvendo, encontraremos:

B → = μ 0 4 π I L i - j

Passo 3

c)

Vamos considerar que o campo magnético resultante é dado por:

B → = B 1 → + B 2 → + B 3 →

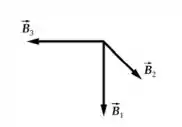
Portanto:

B 1 → = - μ 0 4 π 2 I L ∙ j

B 2 → = μ 0 4 π 2 I L 2 ∙ cos ⁡ 45 ° ∙ i - j = μ 0 4 π 2 I 2 L ∙ ( i - j )

B 3 → = - μ 0 4 π 2 I L ∙ i

Com isso:

B → = B 1 → + B 2 → + B 3 → = - μ 0 4 π 2 I L ∙ j + μ 0 4 π 2 I 2 L ∙ i - j - μ 0 4 π 2 I L ∙ i

Resolvendo, encontraremos:

B → = μ 0 4 π I L - i - 3 j

Resposta

a )   B → = 3 μ 0 4 π I L i - j

b )   B → = μ 0 4 π I L i - j

c )   B → = μ 0 4 π I L - i - 3 j

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere o circuito da Fig. 31-36. Os segmentos curvos são arcos de círculo de raios a e b. Os segmentos retilíneos estão ao longo de raios. Determine o campo magnético B em P, considerando uma corre
Um fio retilíneo longo transporia uma corrente de 50 A. Um elétron está se movendo a 1.0 X 10^7 m/s ao passar a 5.0 cm deste fio. Que força atua sobre o elétron se a sua velocidade estiver orientada (
Cada um dos oito condutores mostrados na Fig. 31-50 transporta uma corrente de 2.0 A para dentro ou para fora da página. Dois caminhos são indicados para a integral de linha $B ds. Qual é o valor da i
Quatro fios longos de cobre estão paralelos entre si a seção transversal do conjunto formando os vértices de um quadrado de 20 cm de lado. Cada fio é percorrido por uma corrente de 20 A, no sentido in
Dois fios longos e paralelos, separados por uma distância d transportam correntes i e 3i no mesmo sentido. Localize o ponto ou os pontos em que seus campos magnéticos se cancelam.