Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 25.1 - Ex. 79
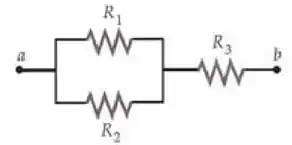
Para a rede mostrada na Figura 25-58, deixe denotar a resistência equivalente entre os terminais a e b. Find (a) , de modo que , (b) , de modo que ; e (c) , de modo que .
Passo 1
Eae galera! Tudo tranquilo? Tendo uma visão geral da coisa, podemos encontrar a resistência equivalente entre os pontos a e b e, em seguida, definir esta resistência igual, por sua vez, para , e e resolver para , e , respectivamente.
Passo 2
Vamo lá. (a) Expressando a resistência equivalente entre os pontos a e b:
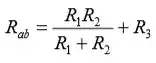
Equilibrando esta expressão a e resolvendo para que R3 a obtenha,
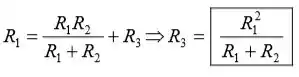
(b) Conjunto R3 igual a Rab:
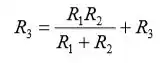
Resolvendo para :
Passo 3
(c) Definir R1 igual a Rab e reescrever o resultado como uma equação quadrática em R1:
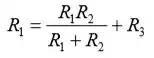
Ou,
Solucionando a equação quadrática para rendimentos de R1:
Resposta
Exercícios de Livros Relacionados
A fonte ideal da Fig. 27-39a tem uma força eletromotriz E = 6,0 V . A curva I da Fig. 27-39b mostra a diferença de potencial V entre os terminais do resistor 1 em função da corrente i no resistor. A e
As duas fontes da Fig. 27-43a são ideais. A força eletromotriz E 1 da fonle 1 tem um valor fixo, mas a força eletromotriz E 2 da fonte 2 pode assumir qualquer valor entre 1,0 V e 10 V . Os gráficos da
Na Fig. 27-50, duas fontes de força eletromotriz ε = 12,0 V e resistência interna r = 0,300 Ω são ligadas em paralelo com uma resistência R . (a) Para que valor de R a potência dissipada no resistor é
O leitor dispõe de um suprimento de resistores de 10 Ω , capazes de dissipar apenas 1,0 W sem serem inutilizados. Qual é o número mínimo desses resistores que é preciso combinar em série ou em paralel
As resistências das Figs. 27-45a e 27-45b são todas de 6,0 Ω e as fontes ideais são baterias de 12 V. (a) Quando a chave S da Fig. 27-45a é fechada, qual é a variação da diferença de potencial V 1 ent