Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 29.Problemas Adicionais - Ex. 67
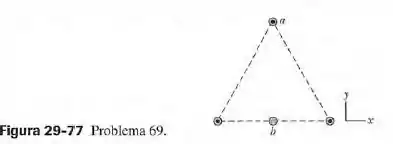
Três fios longos são paralelos ao eixo e conduzem uam corrente de no sentido positivo do eixo . Os pontos de interseção dos fios com o plano formam um triângulo equilátero com de lado, como mostra a figura 29-77. Um quarto fio (fio ) passa pelo ponto médio da base do triângulo e é paralelo aos outros três fios. Se a força magnética exercida sobre o fio é zero, determine (a) o valor e (b) o sentido ( ou ) da corrente no fio .
Passo 1
De acordo com a famigerada regra da mão direita, o campo magnético produzido no ponto pelo fio 1 (esse é o do vértice inferior esquerdo) está no plano e faz um ângulo com o semieixo positivo; o campo produzido no ponto pelo fio (esse é o do vértice inferior direito) também está no plano e faz um ângulo com o semieixo positivo. Por simetria, as componentes dos dois campos se cancelam e as componentes se somam, produzindo um campo resultante que, de acordo com a equação para fios retilíneos longos, é:
Passo 2
Para cancelar esse campo, a corrente do fio deve ter sentido para dentro do papel (ou seja, o sentido ) e um valor absoluto dado por:
na qual é a distância entre o ponto e o ponto .
Passo 3
Como foi dito no item anterior, o sentido do fio é para dentro da página, ou seja, o sentido de .
Resposta
- ;
- O sentido do fio é para dentro da página, ou seja, o sentido de .