Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 29.2 - Ex. 23
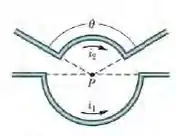
A figura 29-52 mostra dois fios. O fio de baixo conduz uma corrente e inclui um arco de circunferência com de raio e centro no ponto , que subtende um ângulo de . O fio de cima conduz uma corrente e inclui um arco de circunferência com de raio e centro também no ponto P, que subtende um ângulo de . Determine (a) o módulo e (b) a orientação do campo magnético para os sentidos das correntes indicados na figura. Determine também (c) o módulo e (d) a direção de se o sentido da corrente for invertido.
Passo 1
E aí, galerinha! 😁
Nesse problema temos dois fios... O fio de baixo conduz uma corrente e inclui um arco de circunferência com de raio e centro no ponto , que subtende um ângulo de . O fio de cima conduz uma corrente e inclui um arco de circunferência com de raio e centro também no ponto , que subtende um ângulo de . A partir daí queremos determinar o módulo e a orientação do campo magnético para os sentidos das correntes indicados na figura e para o caso do sentido da corrente for invertido.
Tem alguma ideia do que fazemos? 😉
Para descobrirmos o campo magnético no ponto podemos fazer o cálculo por trechos do objeto em questão. A partir disso aplicaremos a superposição dos efeitos dos campos no ponto .
Vamos iniciar olhando as partes retilíneas. A lei de Biot-Savart nos diz o seguinte:
Para os dois elementos retilíneos, o ângulo entre é zero e . Portanto:
Assim, a contribuição de toda a parte reta para o campo magnético é zero. Vamos partir para as partes curvas e aplicar a superposição dos efeitos pra encontrar o campo.
Veja só! 👀
Passo 2
A contribuição dos trechos curvos pode ser calculada usando a seguinte equação:
Mas aqui temos que combinar os efeitos dos campos magnéticos do fio de cima e do fio de baixo, então por superposição temos:
Observa que usamos notações diferentes de corrente e distância pois para cada fio temos uma corrente e um raio .
Antes de somar os campos é importante analisar pra qual direção cada um vai, pra isso pegue a imagem e coloque o seu polegar direito no sentido da corrente como se sua mão envolvesse o fio.
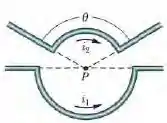
Ao fazer isso você perceberá que a mão entra embaixo do fio 1 e sai no ponto sendo assim pro fio o campo magnético é positivo ou saindo do plano, e pro fio 2 a mão entra no ponto e nesse caso o campo é negativo pra dentro do plano.
Usando o vetor unitário para representar a direção para fora do papel, temos com
O que nos dá .
A orientação do campo magnético é , ou seja, para dentro do papel já que encontramos um valor negativo do campo e adotamos positivo pra fora do papel.
Tranquilo até aqui? 😁
Passo 3
Se invertermos o sinal da corrente temos os dois campos para dentro do papel.
O que nos dá .
E se os dois campos estão entrando no plano a resultante também está, repara que achamos para ela o sinal negativo também.
E aí! o que achou? Responde Aí! 😉
Resposta
- O módulo do campo é ;
- O campo é orientado para dentro do papel;
- O módulo do campo é ;
- O campo é orientado para dentro do papel.