Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 5.1 - Ex. 124

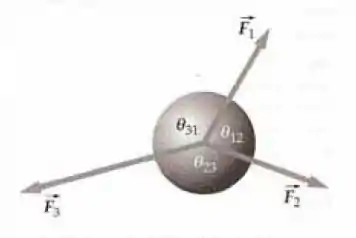
Três forças atuam sobre um corpo em equilíbrio estático (Figura abaixo). (a) Se F 1 ,   F 2 e F 3 representam as magnitudes das forças atuantes sobre o corpo, mostre que F 1 s e n θ 23 = F 2 s e n θ 31 = F 3 s e n θ 12 (b) Mostre que F 1 2 = F 2 2 + F 3 2 + 2 F 2 F 3 c o s θ 23 .

Passo 1

O fato de o objeto estar em equilíbrio estático sob a influência das três forças significa que F 1 → + F 2 → + F 3 → = 0 . Desenhando o triângulo de força correspondente nos permitirá relacionar as forças aos ângulos entre eles pela lei dos senos e pela lei dos cossenos.

Passo 2

Item (a)

Usando o fato de que o objeto está em equilíbrio estático, redesenhando o diagrama de força conectando as forças cabeça-a-cauda:

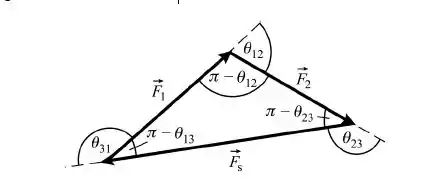
Aplicando a lei dos senos no triângulo:

F 1 s e n π - θ 23 = F 2 s e n π - θ 1 3 = F 3 s e n π - θ 12

Usando a identidade trigonométrica s e n π - α = s e n α :

F 1 s e n θ 23 = F 2 s e n θ 13 = F 3 s e n θ 12

Passo 3

Item (b)

Aplicando a Lei dos Cossenos no triângulo:

F 1 2 = F 2 2 + F 3 2 + 2 F 2 F 3 c o s ⁡ ( π - θ 23 )

Usando a identidade trigonométrica cos ⁡ π - α = - c o s α :

F 1 2 = F 2 2 + F 3 2 + 2 F 2 F 3 c o s θ 23

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma haste rígida isolante, com duas cargas de sinal oposto e módulos diferentes presas às suas extremidades, é colocada em um campo elétrico uniforme E → , como mostrado na figura abaixo. A haste sofr
Na Figura 5.12 vê-se uma pedra de massa m , suspensa por um fio, em uma órbita circular em um plano horizontal. A) Identifique as forças que atuam sobre a pedra. B) Qual é a tensão T no fio? C) Qual é
Como mostra a Figura 5.11, uma pedra gira no ar, presa por um fio de comprimento l . A) Qual é a tensão no fio? (Ignore a gravidade.) B) Se o fio arrebentar quando a pedra estiver na posição mostrada
Uma pedra com massa de 0,80 kg está presa à ponta de um fio com 0,90 m de extensão. O fio se romperá se a tensão ultrapassar 60,0 N. A pedra é girada em um círculo horizontal sobre uma mesa sem atrito
Força sobre o pulso de uma esquiadora. Uma esquiadora de 52 kg gira em torno de um eixo vertical com seu corpo, com os braços esticados horizontalmente; ela faz 2,0 voltas a cada segundo. A distância