Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 10.1 - Ex. 79

A segunda lei de Kepler afirma: a linha que liga o centro do Sol ao centro de um planeta varre áreas iguais em tempos iguais. Mostre que esta lei segue diretamente da lei de conservação da quantidade de movimento angular e do fato de que a força de atração gravitacional entre um planeta e o Sol atua ao longo da linha que liga os centros dos dois corpos celestes.

Passo 1

Olha aqui, fiz a representação da órbita do planeta ao redor do Sol.

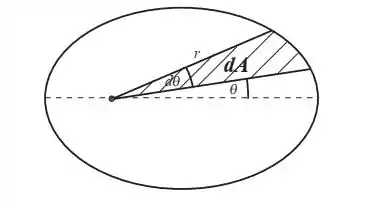
A área desse pedaço de órbita que o planeta andou pode ser calculado como:

Derivando com relação ao tempo:

A variação do ângulo com o tempo é o que chamamos de velocidade angular, ou seja, , e então:

Passo 2

Como a força gravitacional atua ao longo da linha que separa os corpos, ela não produz torque. Se não produz torque, não há variação do momento angular.

Juntando as equações e :

Como queríamos provar!

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um cometa de massa 1,20 × 10 10k g move-se em uma órbita elíptica em torno do Sol. Sua distância do Sol varia entre os intervalos de0,500U A e 50,0U A . (a) Qual é a excentricidade da sua órbita? (b)

O Cometa Halley (Fig. P11.21) aproxima-se do Sol dentro de 0,570U A , e seu período orbital é 75,6a n o s . ( U A é o símbolo da unidade astronômica;1U A=1,50 × 10 11m é a distância média Terra-Sol.)

65 . Estudos sobre a relação do Sol com a nossa galáxia – a Via Láctea – têm revelado que o Sol está localizado próximo da borda externa do disco galáctico, cerca de 30000 anos-luz ( 1a n o - l u z =

64 . O satélite artificial mais antigo em órbita ainda é o Vanguard I, lançado em 3 de março de 1958 . Sua massa é de 1,60k g . Desprezando a resistência do ar, o satélite ainda estaria em sua órbita

62 . Por que a seguinte situação é impossível? Uma nave espacial é lançada em uma órbita circular ao redor da Terra e a circula uma vez por hora.