Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 5.4 - Ex. 43
Uma pedra com massa de está presa à ponta de um fio com de extensão. O fio se romperá se a tensão ultrapassar . A pedra é girada em um círculo horizontal sobre uma mesa sem atrito; a outra ponta do fio permanece fixa. (a) Desenhe um diagrama do corpo livre para a pedra. (b) Ache a velocidade máxima que a pedra pode alcançar sem que o fio se parta.
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente esboçar o diagrama do corpo livre da pedra e encontrar a velocidade máxima que ela pode alcançar sem que o fio se parta.
Uma vez que a pedra viaja em um caminho circular, sua aceleração radial é dada por:
dirigida para o centro do círculo. A única força horizontal na pedra é a tensão do fio. Então, vamos definir a tensão no fio igual ao seu valor máximo, esboçar o nosso diagrama, analisar as forças atuando no movimento através da segunda lei de Newton e calcular a velocidade máxima para essa tensão.
Vamos lá!
Passo 2
a) Vamos começar esboçando o diagrama de corpo livre da pedra:
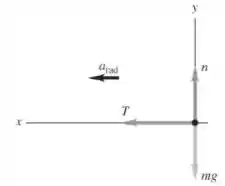
No diagrama, a pedra está em um ponto à direita do centro do caminho.
Como a força normal e a força peso se cancelam, temos apenas forças horizontais atuando no movimento:
Essa força é a força de tração no fio e a aceleração é a aceleração radial igual a . Assim, ficamos com:
Passo 3
b) Isolando nessa equação, vamos ter:
E substituindo os dados do enunciado, obtemos:
A tensão é direcionada para o centro do caminho circular da pedra. A gravidade não tem nenhum papel neste caso porque é uma força vertical e a aceleração é horizontal.
Valeu, galera! Até a próxima! 😉