Três partículas de formam um triângulo equilátero de de lado. As partículas estão ligadas por barras de massa desprezível. Qual é o momento de inércia desse corpo rígido em relação (a) a um eixo que passa por uma das partículas e é paralelo à barra que liga as outras duas, (b) um eixo que passa pelo ponto médio de um dos lados e é perpendicular ao plano do triângulo e (c) um eixo que é paralelo a um dos lados do trângulo e passa pelos pontos médios dos outros dois lados?
Passo 1
Vamos fazer um desenho da situação:
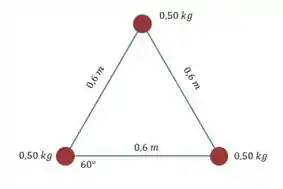
Em cada um dos casos, para calcular o momento de inércia, vamos ter que usar essa fórmula aqui:
Onde é a distância da partícula até o eixo escolhido.
Passo 2
(a) O primeiro eixo passa por uma das partículas, e é paralelo à barra que liga as outras duas:
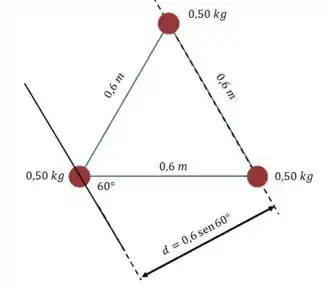
A partícula que passa pelo eixo tem momento de inércia nulo, já que , e para as outras duas a distância é igual:
Passo 3
(b) Agora o eixo é perpendicular ao plano da página. Vamas desenhar apenas o ponto onde ele cruza o plano.
Como o triângulo é equilátero, podemos desenhar o eixo em qualquer um dos seus lados:
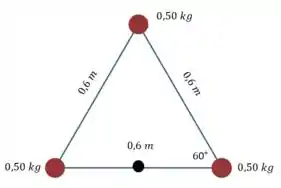
A distância das duas partículas de baixo é mais fácil de calcular:
E a distância até a partícula de cima pode ser calculada usando aquele ângulo de no canto direito:
Então o momento de inércia é:
Passo 4
(c) Por último, temos um eixo paralelo a um dos lados, e passando pelo ponto médio dos outros dois:
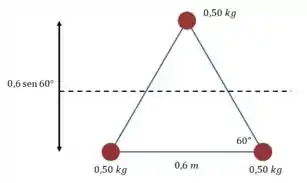
Agora a distância do eixo até cada uma das esferas é igual à metade da altura do triângulo equilátero:
Então o momento de inércia é:
Resposta
(a) .
(b) .
(c) .