Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 10.6 - Ex. 34

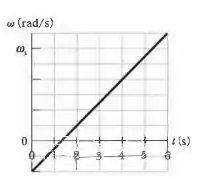
A Fig. 10-30 mostra a velocidade angular em função do tempo para uma barra fina que gira em torno de uma das extremidades. A escala do eixo ω é definida por ω s = 6,0   r a d / s . (a) Qual é o módulo da aceleração angular da barra? (b) Em t =   4,0   s , a barra tem uma energia cinética de 1,60   J . Qual é a energia cinética da barra em t   = 0 ?

Passo 1

(a) Vamos olhar para o gráfico de novo:

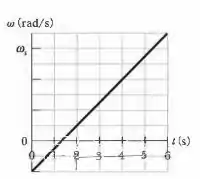
Como ω s = 6   r a d / s e ele está a 6 quadradinhos acima da origem, cada quadradinho vale 1   r a d / s , ok?

Bom, além disso, sabemos que a aceleração é a primeira derivada da velocidade. Logo, se queremos calcular a aceleração angular desse movimento no gráfico, vamos achar a primeira derivada dele... Mas como é uma reta, a derivada da reta é o próprio coeficiente angular!! Chamando a acelereção angular de α :

α   = 9 6   =   1,5   r a d / s 2 .

Porque são 6 quadradinhos na horizontal e 9 na vertical, show??

Passo 2

(b) Então, como a barra está apenas girando em torno de uma das suas extremidades, teremos apenas a energia cinética de rotação K r o t , que é:

K = K r o t = I ω 2 2

Onde I é o momento de inércia da barra.

Como a velocidade angular no instante t   =   0 é – 2   r a d / s :

K 0 = I - 2 2 2 = 2 I

Passo 3

E como a velocidade angular no instante t   =   4   s é 4   r a d / s e K = 1,6 J nesse mesmo instante:

K = 1,6 = I 4 2 2 = 8 I

8 I = 1,6

I = 0,2

Substituindo o valor de I na equação para K em t = 0 :

K 0 = 2 I

K 0 = 2 × 0,2

∴

K 0 = 0,4 J

Resposta

(a) α   =   1,5   r a d / s 2

( b ) K 0 = 0,4 J

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma roda tem um aro fino de 3,0 k g e quatro raios, cada um com 1,2 k g de massa. Determine a energia cinética da roda quando rola a 6,0 m / s sobre uma superfície horizontal.
Determine a aceleração angular do cilindro do problema 96. Ele gira no sentido horário ou anti-horário? (b) Qual é a aceleração linear do cilindro (magnitude e orientação) em relação à mesa? (c) Qual
Como engenheiro-chefe de projetos de uma grande fábrica de brinquedos, você deve projetar um brinquedo tipo montanha-russa. A idéia, como mostrada na figura, é que a bolinha de massa m e raio r deve d
Se a força do problema 96 atua ao longo de uma distância d , forneça, em termos dos símbolos, (a) a energia cinética da barra e (b) a energia cinética total do cilindro. (c) Mostre que a energia cinét
Uma bola de boliche, de massa M e raio R , é lançada de forma que, ao atingir o piso, está se movendo horizontalmente com um rapidez v 0 , sem girar. Ela desliza uma distância s durante um tempo t ant