Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 1.Problemas - Ex. 57
Os vetores e têm módulos iguais de . A soma de e é o vetor . Determine o ângulo entre e .
Passo 1
E aiii gente, tudo bom com vocês?
Vamos fazer mais uma questãozinha aqui?
Vem comigo!
Como , temos:
Como os vetores têm a mesma magnitude e componentes x de magnitude igual, mas de sinal oposto, os vetores são reflexos de um ao outro no eixo y, conforme mostrado no diagrama abaixo:
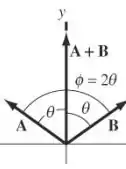
Passo 2
Portanto, os dois vetores têm os mesmos componentes y:
Definindo como o ângulo entre e o eixo y, é visto que:
O ângulo entre é então .
Resposta
O ângulo entre é .
Exercícios de Livros Relacionados
Uma partícula sofre três deslocamentos sucessivos em um plano: d 1 →,4,00m para sudoeste, d 2 → , 5,00 para leste, e d 3 →,6,00 em uma direção 60,0 ° ao norte do leste. Use um sistema de coordenadas c
Um vetord → tem módulo 2,5m e aponta para o norte . Determine (a) o módulo e (b) a orientação de 4,0 d → . Determine (c) o módulo e (d) a orientação de - 3,0 d → .
Se a → - b → = 2c → , a → + b → = 4 c → e c → = 3 i ^ + 4 j ^ , determine (a) a → e (b) b →
Um banco no centro de Boston é assaltado (veja o mapa da Fig. 3-36). Os bandidos fogem de helicóptero e, tentando despistar a polícia, fazem três voos em sequência, descritos pelos seguintes deslocame
Uma roda com 45,0c m de raio rola sem escorregar em um piso horizontal (veja a figura). No instante t 1 , o ponto P , pintado na borda da roda, está no ponto de contato entre a roda e o piso; Em um in