Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 1.Problemas - Ex. 66
Uma mulher que deseja saber a altura de uma montanha mede o ângulo de elevação desta como . Após caminhar para mais perto da montanha em terreno plano, ela encontra um ângulo de.
a) Faça um desenho do problema, desprezando a altura dos olhos da mulher acima do chão. Dica: Utilize dois triângulos.
b) Usando o símbolo para representar a altura da montanha e para indicar a distância original da mulher à montanha, desenhe esquematicamente a figura.
c) Usando a figura desenhada, escreva duas equações trigonométricas relacionando as duas variáveis selecionadas.
d) Encontre a altura .
Passo 1
Vamos fazer o desenho esquemático que vai servir bem pra a) e b). De acordo com o enunciado, vai ficar mais ou menos assim, de modo simplificado:
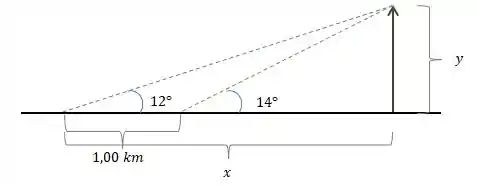
Imaginando que a seta preta na vertical, de tamanho , represente a distância do chão até o pico da montanha, considerando os ângulos medidos e a distância locomovida pela topógrafa, já somos capazes de responder c) e d).
Passo 2
c) Precisamos de 2 equações que correlacionem as distâncias e . Dá pra fazer isso tranquilamente a partir da tangente dos ângulos da figura.
A partir do ângulo de , podemos escrever:
E a partir do ângulo de , escrevemos:
Aqui, é a distância entre a topógrafa e a montanha quando ela se desloca 1,00 km pra frente e mede o ângulo de , certo?!
Passo 3
d) Por fim, vamos determinar a altura da montanha, , a partir das duas equações escritas no Passo 2. Trabalhando em cima delas, podemos escrever o seguinte:
Bem como:
Vamos igualar as duas equações que descrevem , assim:
Juntamos os termos que contêm e vamos ter:
Agora, com o valor de determinado, conseguimos calcular tranquilamente por uma das duas equações do Passo 2. Vamos pegar a primeira e resolver:
Substituindo por seu valor determinado, vamos ter:
ou
Resposta
ou