Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 3.Problemas Adicionais - Ex. 69
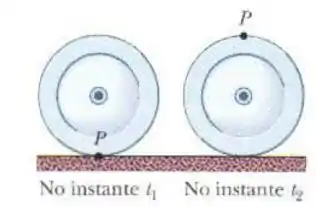
Uma roda com de raio rola sem escorregar em um piso horizontal (veja a figura). No instante , o ponto , pintado na borda da roda, está no ponto de contato entre a roda e o piso; Em um instante posterior , a roda descreveu meia revolução. Quais são (a) o módulo e (b) o ângulo (em relação ao piso) do deslocamento do ponto ?
Passo 1
Belezoca galerinha, pra gente encontrar o vetor do deslocamento do ponto , precisamos fazer lembrar da relação de distância, dada na forma vetorial como:
Ou seja, temos que considerar a diferença dos vetores da posição do ponto nos instantes e .
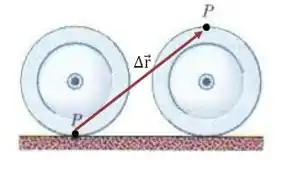
Não importa qual ponto nós escolhermos como origem do nosso sistema, essa diferença sempre vai ser um vetor que liga as posições inicial e final do ponto de maneira igual na figura dada abaixo:
Passo 2
Como a roda descreveu meia revolução entre os dois instantes: a distância horizontal percorrida foi:
E já a distância vertical percorrida pelo ponto é igual a , ou seja:
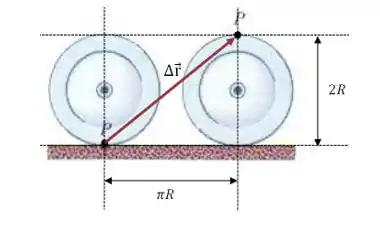
E agora começou a ficar bonitinho, porque saca só, as duas distâncias que descobrimos, formam os catetos do triângulo retângulo de hipotenusa , sendo assim, podemos calcular o módulo do vetor usando o teorema de pitágoras:
Logo:
Como , obtemos:
Passo 3
E agora, para calcular o ângulo que o vetor forma com o piso, podemos lembrar da definição da tangente num triângulo retângulo, dada como:
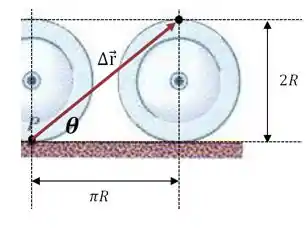
Logo:
Resposta
(a) O módulo do deslocamento é .
(b) O ângulo do deslocamento em relação ao piso é .