Você atira para cima uma bola de até uma altura de .
(a) Use um valor razoável para o deslocamento da bola enquanto ela está na sua mão, para estimar o tempo em que ela fica na sua mão, enquanto você a está atirando.
(b) Calcule a força média exercida por sua mão enquanto você atira a bola. (É razoável desprezar a força gravitacional sobre a bola enquanto ela está sendo atirada?)
Passo 1
A imagem representa a bola durante o intervalo de tempo em que você exerce uma força nela para acelerá-la para cima. A força média exercida pode ser determinada pela variação da quantidade de movimento da bola. A variação de velocidade pode ser encontrada aplicando a conservação de energia mecânica no sistema que contém a Terra e a bola após sair da sua mão.
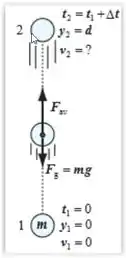
Passo 2
(a) Relacionando o deslocamento da mão com a velocidade média da bola na mão e o tempo que ela fica na sua mão:
E agora, aplicando a conservação de energia mecânica:
Mas como as energia cinética final e potencial gravitacional inicial valem zero, , então só nos resta:
Substituindo e pelas variáveis da figura e isolando :
Queremos o tempo que a bola fica na nossa mão. Sendo assim, como :
Passo 3
Assumindo como valor razoável para o deslocamento da mão sendo de e substituindo por valores numéricos as variáveis da equação , chegamos em:
Passo 4
(b) Vamos relacionar a força média exercida pela mão na bola com a variação da quantidade movimento:
Mas como , logo , e então temos que:
Lembrando de que que já foi calculada no item (a) e agora basta trocar na equação acima:
Mudando as variáveis pelos números adequados:
Passo 5
Para verificar se podemos desprezar a força gravitacional enquanto a bola é atirada para cima, vamos expressar a razão entre a força gravitacional e a força média:
Trocando os valores numéricos:
Verificamos que a força gravitacional é menor do que da força média atuante na bola, portanto é aceitável ignorá-la nos cálculos.
Resposta
(a)
(b) . A força gravitacional é menor do que da força média atuante na bola, portanto é aceitável ignorá-la nos cálculos.