Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 8.1 - Ex. 47
Uma bola de , movendo-se com uma rapidez de , atinge uma parede a um ângulo de com a normal, rebate e volta com a mesma rapidez e o mesmo ângulo. Ela permanece em contato com a parede durante . Qual é a força média exercida pela bola sobre a parede
Passo 1
Esquematização do problema:
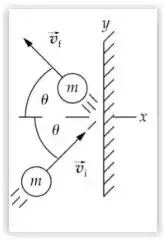
A figura mostra a bola imediatamente antes e depois da colisão. Escolhendo o sentido positivo do eixo como sendo para direita. O muro muda a quantidade momento linear da bola exercendo uma força sobre ela durante a colisão. A reação dessa força é a força que a bola exerce sobre o muro. Como são forças de ação e reação, elas têm a mesma magnitude, a qual pode ser calculada pela variação de momento linear da bola.
Passo 2
Usando a Lei de Newton, podemos relacionar a força média exercida pela parede com a força média exercida pela bola:
Agora, relacionando a força média exercida pela parede na bola com a mudança da quantidade de movimento:
Expressando em função de suas componentes:
Mas, como :
.
Sabendo que e , temos que:
Passo 3
Substituindo a equação na :
Finalmente, basta trocar pelos valores numéricos pertinentes a cada variável para calcular o módulo do vetor :
Resposta
A força média exercida pela bola sobre a parede é de: