Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 8.1 - Ex. 40

Uma cunha de massa M é colocada sobre uma superfície horizontal e sem atrito, e um bloco de massa m é colocado sobre a cunha, que também tem uma superfície sem atrito (figura abaixo). O centro de massa do bloco desce de uma altura h , enquanto o bloco desliza de sua posição inicial até o piso horizontal.

(a) Quais são os valores de rapidez do bloco e da cunha, no instante em que se separam, seguido seus próprios caminhos?

(b) Teste a plausibilidade dos cálculos para caso o limite M ≫ m .

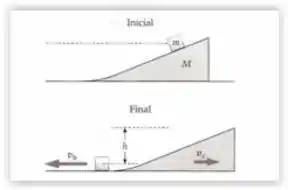
Passo 1

(a) Primeiro, vamos definir o sistema como sendo a Terra, o bloco e a cunha. Então, aplicaremos a conservação de energia e conservação de momento linear.

Passo 2

Aplicando a conservação de energia sem forças dissipativas, temos:

∆ K + ∆ U = 0

Onde ∆ K é a variação de energia cinética e ∆ U é a variação de energia potencial.

Como K i =   U f = 0 e escrevendo a notação " b " para o bloco e " c " para a cunha:

K b , f +   K c , f -   U b , i =   0

1 2 m v b 2 +   1 2 M v c 2 - m g h = 0   ( I )

Passo 3

Aplicando a conservação de momento linear do sistema, sabendo que ele partiu do repouso:

∆ p → s i s t = ∆ p → b + ∆ p → c = 0

Mas como p → b , i =   p → c , i = 0

- m v b i ^ + M v c i ^ = 0

Em seguida, isolamos v c :

m v b i ^ = M v c i ^

v c =   m M v b   ( I I )

Passo 4

Substituindo v c da equação ( I I ) na equação I , obtemos a seguinte relação:

1 2 m v b 2 +   1 2 M m M v b 2 - m g h = 0

Isolando v b e rearranjando temos:

1 2 m v b 2 +   1 2 M m M v b 2 = m g h

m v b 2 + m 2 M v b 2 = 2 m g h

v b 2 m M + m 2 M = 2 m g h

v b 2 = 2 m M g h m M + m 2

v b 2 = 2 M g h M + m

v b =   2 g h M M + m   ( I I I )

Substituindo v b na equação ( I I ) , chegamos a:

v c =   m M v b

v c =   m M 2 g h M M + m

v c =   2 g h m 2 M ( M + m )   ( I V )

Passo 5

(b) Agora vamos Reescrever a equação ( I I I ) , dividindo o numerador e denominador do radicando por M :

v b =   2 g h M M M + m M

v b =   2 g h 1 +   m M

Mas quando M   ≫ m , m M → 0 . Logo, ficamos com:

v b ≈   2 g h

Em seguida, vamos reescrever a equação ( I V ) , dividindo o numerador e denominador do radicando por M :

v c =   2 g h m 2 M M M + m M

v c =   2 g h m M 2 1 +   m M

Mas quando M   ≫ m , m M → 0 .   Logo, ficamos com:

v c ≈ 0

Resposta

a) A rapidez do bloco é igual a v b =   2 g h M M + m e a rapidez da cunha é v c =   2 g h m 2 M ( M + m ) .

b) Quando M ≫ m , v b ≈   2 g h   e v c ≈ 0 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma pulga de massa igual a 2mg é capaz de saltar verticalmente a uma altura de 50cm. Durante o intervalo de tempo ( muito curto ) em que estica as patas para impulsionar o salto, ela se eleva de 1mm a
Tiago, um adolescente de 85k g , salta da borda de um cais horizontal até um bote de 150k g que flutuava livremente, inicialmente em repouso. O bote, então, com o passageiro dentro, se do cais a 2,0m
Uma mulher de 55k g , participando de um reality show de televisão, se encontra na extremidade sul de um bote de 150k g que flutua em águas infestadas de crocodilos. Ela e o bote estão inicialmente em
Um corpo de 5,0k g e outro de 10,0k g , ambos sobre uma mesa sem atrito, estão ligados por uma mola comprimida sem massa. A mola é liberada e os corpos são lançados em sentidos opostos. O corpo de 5,0
A figura abaixo mostra o comportamento de um projétil logo após ele ter se partido em três pedaços. Qual era a rapidez do projétil logo antes de se partir? av 3 bv 3 / 3 cv 3 / 4 d4 v 3 e( v 1 +v 2 +v