Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 1.1 - Ex. 78

Você vê um avião que está a 1,50   k m norte, 2,5   k m leste, e a uma altitude de 5,0   k m acima da sua posição. (a) A que distância de você está o avião? (b) Em qual ângulo a partir do norte (no plano horizontal) está sua linha de visão? (c) Determine o vetor posição do avião (a partir da sua localização) em termos dos vetores unitários, colocando i ^ na direção leste, j ^ na direção norte, e k ^ na vertical para cima. (d) A qual ângulo de elevação (acima do plano horizontal da Terra) está o avião?

Passo 1

a) Vamos entender a situação posicionando você e o avião num sitestema de coordenadas cartesiano. Imagina que você está na origem, em P = 0,0 , 0 . A direção norte vai ser a direção y , a direção leste vai ser a direção x , e a altitude vai ser a direção z .

Então, o avião estaria no ponto A = 2 , 5 ,     1 , 5 ,     5   k m .

Para calcular a distância até o avião, nós podemos achar o vetor que sai de você e vai até o avião, e calcular o módulo desse vetor!

Para calcular o vetor, a gente vai fazer a coordenada final dele, ou seja, A , menos a coordenada inicial P :

u → = A - P = 2.5 ,   1.5 ,   5 - 0,0 , 0 = 2 . 5 ,   1 . 5 ,   5

Aí a distância entre esses dois pontos, ou seja, a distância entre você e o avião é o módulo de u → :

d = u → = 2 , 5 2 + 1 , 5 2 + 5,0 2

d = 5,8   k m

Passo 2

(b) Em seguida queremos saber qual é o ângulo a partir do norte (no plano horizontal) formado pela nossa linha de visão até o avião. Ou seja, qual ângulo que a projeção do nosso vetor u → em x y faz com o eixo y (norte).

Como estamos pensando apenas no plano horizontal, esse é o ângulo formado pelas distâncias de 1,5   k m e 2,5   k m :

θ = arctan ⁡ 2,5 1,5 = 59 °

Passo 3

(c) O avião está a 2,5   k m na direção leste (direção i ^ ), 1,50   k m na direção norte (direção j ^ ) e 5,0   k m na vertical para cima (direção k ^ ).

Então podemos escrever o vetor posição do avião da seguinte forma:

r → = 2,5   i ^ + 1,5   j ^ + 5,0   k ^   k m

Passo 4

(d) Imagine que d é o comprimento da linha que liga você diretamente ao avião (e que nós já calculamos) e que d H é a projeção dessa linha no plano horizontal.

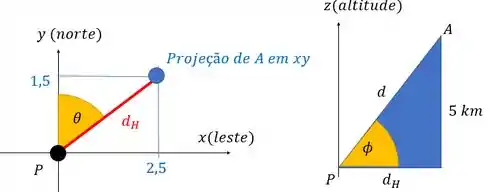
Nesse caso podemos usar o teorema de Pitágoras para calcular d H , é só considerar as duas distâncias horizontais que foram dadas no enunciado:

d H = 2,5 2 + 1,5 2 = 2,91   k m

E o ângulo de elevação é o ângulo que essa linha forma (um cateto) forma com a linha d que liga você direto ao avião. O outro cateto desse triângulo retângulo é a altitude h , então o ângulo de elevação é:

ϕ = arctan ⁡ h d H

ϕ = arctan ⁡ 5,0 2,91 ≅ 60 °

Resposta

(a) d = 5,8   k m .

(b) θ = 59 ° .

(c) r → = 2,5   i ^ + 1,5   j ^ + 5,0   k ^   k m .

(d) ϕ = 60 ° .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os três vetores na Fig. 3-33 têm módulos a=3,00m , b=4,00m e c=10,0m ; θ = 30,0 ° . Determine (a) a componente x e (b) a componente y de a → ; (c) a componente x e (d) a componente y de b → ; (e) a co
Um jogador de golfe precisa de três tacadas para colocar a bola no buraco. A primeira tacada lança a bola 3,66m para o norte, a segunda 1,83m para sudeste e a terceira 0,91m para sudoeste . Determine
Um vetor   d → tem módulo 2,5   m e aponta para o norte . Determine (a) o módulo e (b) a orientação de 4,0 d → . Determine (c) o módulo e (d) a orientação de - 3,0 d → .
Se B → é somado a A → , o resultado é 6 ,   0 i ^ + 1 ,   0 j ^   . Se B → é subtraído de A → , o resultado é - 4,0 i ^   + 7,0 j ^ . Qual é o módulo de A → ?
Se a → - b → = 2c → , a → + b → = 4 c → e c → = 3 i ^ + 4 j ^ , determine (a) a → e (b) b →