Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 3.Problemas - Ex. 77
Você construiu uma pistola de batatas acionada por spray de cabelo e deseja descobrir a velocidade de disparo v0 das batatas, a velocidade que elas alcançam ao sair do cano da pistola. A mesma quantidade de spray é utilizada a cada disparo da arma, e você confirmou,
por disparos repetidos a mesma altura, que a velocidade do disparo é aproximadamente a mesma para cada tiro. Você sobe em uma torre de transmissão de micro-ondas (com permissão, é claro) para disparar as batatas horizontalmente em diferentes alturas acima do solo. Seu amigo mede a altura do cano da pistola acima do solo e o alcance R de cada batata. Os seguintes dados são obtidos:
Cada um dos valores de h e R tem algum erro de medição: a velocidade do disparo não é exatamente a mesma a cada tentativa, e o cano não é exatamente horizontal. Assim, você usa todas as medições para conseguir a melhor estimativa de v0. Não há vento soprando, de modo que você decide desprezar a resistência do ar. Você usa g 9,80 m/s2 em sua análise. (a) Selecione um modo de representar os dados como uma linha reta. (b) Use a inclinação da linha com melhor ajuste do item (a) para calcular o valor médio de v0. (c) Qual seria o alcance horizontal de uma batata disparada a partir do nível do solo a um ângulo de 30,0º acima da horizontal? Use o valor de v0 que você calculou no item (b).
Passo 1
A tabela fornece dados que mostram a extensão horizontal da batata para várias alturas de lançamento. Você deseja usar essas informações para determinar a velocidade de lançamento da batata, assumindo a resistência do ar insignificante.
As batatas são lançadas horizontalmente, então , e elas estão em queda livre, então para baixo e . O tempo que uma batata está no ar é apenas o tempo que leva para cair verticalmente do ponto de lançamento para o solo a uma distância h.
Passo 2
Letra a:
Para o movimento vertical de uma batata, temos . O alcance horizontal R é dado por . Elevando ao quadrado temos:
Representando graficamente versus h, teremos uma linha reta com inclinação . O resultado é mostrado na figura.
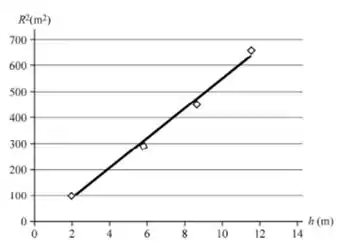
Passo 3
Letra b:
A inclinação do gráfico é 55.2m, então
Passo 4
Letra c:
Neste caso, as batatas são lançadas e pousam no nível do solo, então podemos usar a fórmula de intervalo com e O resultado é:
Esta abordagem para encontrar a velocidade de lançamento requer apenas medições simples: o alcance e a altura de lançamento. Seria difícil e exigiria um equipamento especial para medir diretamente.
Resposta
- Ver gráfico