Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 4.Problemas Adicionais - Ex. 122

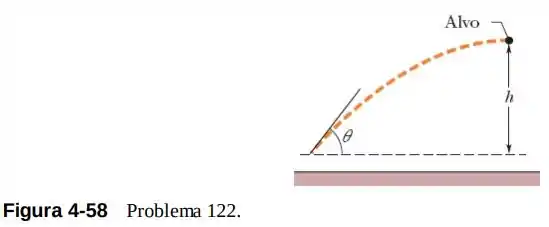
122- Você pretende lançar uma bola com uma velocidade escalar de 12,0 m / s em um alvo que está a uma altura h = 5.00   m acima do ponto de lançamento (Fig. 4-58). Você quer que a velocidade da bola seja horizontal no instante em que ela atingir o alvo. (a) Com que ângulo θ acima da horizontal você deve atirar a bola? (b) Qual é a distância horizontal do ponto de lançamento até o alvo? (c) Qual é a velocidade escalar da bola no momento em que ela atinge o alvo?

Passo 1

Pelo enunciado da questão conseguimos extrair informações valiosas para responder a questão, tais como na altura de h = 5 a bola para de subir verticalmente tendo somente a velocidade horizontal na sua componente ( que por sinal sempre será constante).

Para encontrar a velocidade de lançamento sem a necessidade de descobrir de antemão o tempo de subida nós precisamos aplicar a equação de Torricelli, que tem a cara.

v 2 = v 0 2 + 2 a Δ s

Onde a aceleração é o da gravidade que e é decrescente, logo:

v 2 = v 0 2 - 2 g Δ s

Como a velocidade uniformemente acelerada (variante) é a velocidade de y logo:

v y 2 = v 0 y 2 - 2 g Δ s

Substituindo os valores com os dados que a questão nos fornece nós teremos:

0 = v 0 y 2 - 2 × 9.81 × 5

v 0 y = 2 × 9.81 × 5 = 9.9   m / s

Passo 2

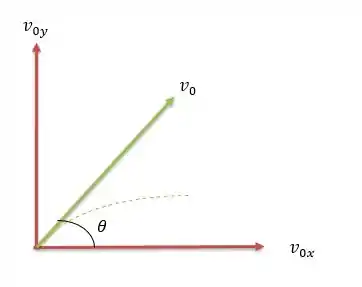
  1. Dando um zoom no ponto de origem nós conseguimos decompor a velocidade inicial em duas componentes.

    2. Logo o valor de v 0 y   será igual a:

    v 0 y = v 0 c o s ( 90 - θ )

    v 0 y =   v 0 s e n   θ

    Onde v 0 = 12   m / s . Logo:

    9.9 = 12   s e n   θ

    θ = s e n - 1 9.9 12 → θ = 55.59 °

    Passo 3

  2. Em um lançamento oblíquo nós consideramos a velocidade horizontal como constante e por conta disso a distância s pode ser calculada da seguinte forma:

    3. s = v x t

    Assim como encontramos a componente vertical no passo anterior nós podemos encontrar a horizontal rebatendo o vetor v 0 para baixo, logo:

    v x = v 0 cos ⁡ θ

    E o tempo encontra-se pela equação de definição da aceleração:

    a = Δ v Δ t

    Como o tempo inicial é de 0   s temos:

    v f - v 0 = a t

    v f = v 0 + a t

    Como a aceleração é a da gravidade e ela é decrescente temos o tempo t igual a:

    v f = v 0 - g t

    t = v f + v 0 g

    Como a velocidade final no ponto de maior altura é v y = 0 logo:

    t = v 0 y g = 9.9 9.81 = 1.01   s

    Então a distância horizontal percorrida pela bola será de:

    s = v 0 c o s   θ × t = 12   c o s 55.59 × 1.01 = 6.85   m

    Passo 4

  3. Como foi discutido no momento em que ela atinge o alvo a condição para que ela fique totalmente na horizontal é que a bola pare de crescer na vertical ou:

v y = 0

Logo a única componente possível é a componente horizontal, que não é afetada pela gravidade, logo:

v = v 0 x = v x = 12 cos ⁡ 55.56 = 6.78   m / s

Resposta

a )   55.56 °

b )   6.85   m

c )   6.78   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma pedra é atirada do topo de um edifício de 20 m de altura a um ângulo de 53° acima da horizontal. (a) Se o alcance horizontal é igual à altura do prédio, com que rapidez a pedra foi atirada? (b) Qu
Se um projétil que abandona a arma a 250 m/s deve atingir um alvo 100 m à frente, no memso nível da arma (1,7 m acima do nível do chão), a arma deve apontar para um ponto acima do alvo. (a) A que altu
Um avião de carga perdeu um pacote em vôo porque alguém esqueceu de fechar as portas traseiras do compartimento de carga. Você é membro da equipe de especialistas em segurança encarregada de analisar
Duas bolas são atiradas com a mesma rapidez do topo de um penhasco de altura h . Uma bola é atirada a um ângulo α acima da horizontal. A outra bola é atirada a um ângulo β abaixo da horizontal. Mostre
Uma pequena bola de aço é projetada horizontalmente de cima de um longo lance de escada. A rapidez inicial da bola é de 3,0 m/s. Cada degrau tem uma altura de 0,18 me uma largura de 0,30 m. Qual é o p