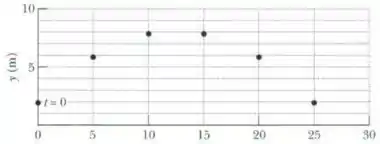
Uma competição de atletismo é realizado em um planeta de um sistema solar distante. Um arremessador de peso lança o peso de um ponto acima do nível do solo. Um gráfico estroboscópico da posição do peso aparece na figura, onde as leituras foram tomadas a cada e o peso foi arremessado no instante . (a) Qual é a velocidade inicial do peso, em termos dos vetores unitários? (b) Qual é o módulo da aceleração em queda livre no planeta? (c) Quanto tempo após ter sido arremessado o peso toca o solo? (d) Se um arremesso de peso for feito na Terra nas mesmas condições, quanto tempo após o lançamento o peso tocará o solo?

(a) Para encontrar os valores de e vamos usar o sexto ponto do gráfico, que tem coordenadas ) e corresponde ao instante .

Começando por :

E agora . Perceba que nesse quinto ponto :

Como não sabemos a aceleração da gravidade no planeta, precisamos de mais um ponto para encontrar . Por exemplo, quanto , :

Substituindo o primeiro resultado nesse, ficamos com:

Então o vetor velocidade inicial é:

(b) E agora podemos calcular também o módulo da acelerção nesse planeta:

(c) Quando o peso toca o solo, temos . Então vamos escrever a função que dá em função do tempo:

E podemos resolver essa equação do segundo grau:

E como só a raiz positiva tem significado nesse caso:

(d) Agora queremos fazer a mesma conta que acabamos de fazer, mas usando a aceleração da gravidade na superfície da Terra:

Então:

E podemos resolver essa equação do segundo grau:

E como só a raiz positiva tem significado nesse caso: