Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 17.1 - Ex. 49
Você copia o seguinte parágrafo de um livro de física marciano:
"1 snorf de um gás ideal ocupa um volume de 1,35 Zaks. A uma temperatura de 22 glips, o gás tem uma pressão de 12,5 klads. A uma temperatura de – 10 glips, o mesmo gás agora tem uma pressão de 8,7 klads."
Determine a temperatura do zero absoluto em glips.
Passo 1
THERE’S A STARMAN WAITING IN THE SKY...Opa, nem te vi aí, tava aproveitando esse clima marciano para cantar esse clássico ;) MAS ENFIM, eu sei que você está aqui para entender como resolver essa questão, então meu bem, ENTRA NA MINHA NAVE E SEGUE O FLUXO, que é sucesso, simbora!
Primeiramente, sabemos que esse gás marciano é ideal, ou seja, a pressão dele aumenta dependendo do quanto a temperatura aumenta, ou seja, a pressão e a temperatura são diretamente proporcionais, meu consagrado, logo, um gráfico da Pressão pela Temperatura será linear, ou seja, teremos uma função afim () envolvendo a Pressão e Temperatura, e com isso, conseguiremos resolver a questão mais rápido que a millenium falcon, BORA ANALISAR ESSE GRÁFICO:
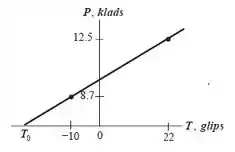
Primeiramente, teremos que achar as componentes a e b da função afim, bem, sabemos que , logo, basta obter a variação do eixo y e a variação do eixo x:
AGORA BASTA SUBSTITUIR QUE TEREMOS:
0,11875
AGORA TEMOS O COEFICIENTE ANGULAR DA NOSSA FUNÇAÕ AFIM!!!
Passo 2
Agora que temos o coeficiente angular, precisamos do valor do termo constante, para isso, usaremos a própria função afim:
Agora, usaremos uma pressão e uma temperatura que já sabemos que estão relacionadas:
PROTINHO, agora temos todos os termos da nossa função afim, SEGUIREMOS PARA A CONCLUSÃO!
Passo 3
A nossa função afim ficou com essa cara:
Sabemos que o zero absoluto possui uma Pressão igual à zero, portanto, basta igualar a pressão da nossa função para zero e calcular a Temperatura, que, consequentemente, será a temperatura do zero absoluto em glips (Marcianos são criativos com nomes).
PRONTINHO, essa questão é das boas, é isso, É SÓ ISSO, muito bom ter sua companhia até aqui, volte mais vezes ;) BONS ESTUDOS!