Enunciado
Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 33.Problemas - Ex. 47
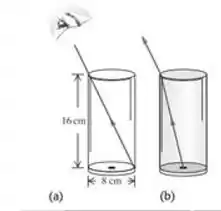
Você olha para dentro de um recipiente de vidro com paredes verticais de modo que o seu olhar vá da borda superior até a extremidade oposta no fundo (Figura 33.48a). O recipiente é um cilindro oco com paredes finas de altura de com diâmetro superior e inferior de . Enquanto você mantém seus olhos fixos na mesma posição, um amigo enche o recipiente com um líquido transparente, e a seguir você vê uma moeda de um centavo que está no centro do recipiente (Figura 33.48b). Qual é o indice de refração do líquido?
Passo 1
Primeiro, vamos analisar o caso sem o líquido. Nessa situação, a lei de snell nos diz:
Podemos calcular o pela geometria. Usando o triângulo retângulo temos:
Então
Voltando para a lei de snell:
Portanto
Show! Isso porque estamos considerando o caso em que o cilindro está vazio.
Passo 2
Agora, vamos ver como fica a lei de snell quando enchemos o cilindro com o liquido
Podemos calcular o usando a geometria.
Então
Voltando para a lei de snell:
Então:
Show!